To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
XY modelLike the famous Ising and Heisenberg models, the XY model is one of the many highly simplified models in the branch of physics known as statistical mechanics. It is a special case of the n-vector model. In the XY model, 2D classical spins Product highlightwhere the sum runs over all pairs of neighboring spins and The continuous version of the XY model is often used to model systems that possess order parameters with the same kinds of symmetry, e.g. superfluid helium, hexatic liquid crystals. Topological defects in the XY model leads to a vortex-unbinding transition from the low-temperature phase to the high-temperature disordered phase. In two dimensions the XY model exhibits a Kosterlitz-Thouless transition from the disordered high-temperature phase into the quasi-long range ordered low-temperature phase. See also
References
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "XY_model". A list of authors is available in Wikipedia. |


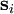 are confined to some lattice. The spins are 2D unit vectors that obey O(2) (or U(1)) symmetry, (as they are classical spins). Mathematically, the Hamiltonian of the XY model
with the above prescriptions is given by the following:
are confined to some lattice. The spins are 2D unit vectors that obey O(2) (or U(1)) symmetry, (as they are classical spins). Mathematically, the Hamiltonian of the XY model
with the above prescriptions is given by the following:
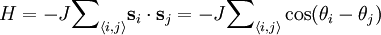



 denotes the standard Euclidean inner product.
denotes the standard Euclidean inner product.


