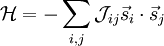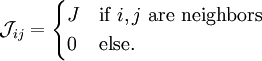To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Heisenberg model (classical)The Heisenberg model is the n = 3 case of the n-vector model, one of the models used in statistical physics to model ferromagnetism, and other phenomena. Product highlightIt can be formulated as follows: take a d-dimensional lattice, and a set of spins of the unit length
each one placed on a lattice node. The model is defined through the following Hamiltonian: with a coupling between spins. The general mathematical formalism used to describe and solve the Heisenberg model and certain generalizations is developed in the article on the Potts model. See alsoCategories: Condensed matter physics | Lattice models |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Heisenberg_model_(classical)". A list of authors is available in Wikipedia. |





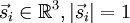 ,
,