To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Kosterlitz-Thouless transitionThe Kosterlitz-Thouless transition, or Berezinsky-Kosterlitz-Thouless transition, is a special transition seen in the XY model for interacting spin systems in 2 spatial dimensions. The XY model is a 2-Dimensional vector spin model that possesses U(1) or circular symmetry. This system is not expected to possess a normal second order phase transition. This is because the expected ordered phase of the system is destroyed by transverse fluctuations, i.e the Goldstone modes (see Goldstone boson) associated with this broken continuous symmetry, which logarithmically diverge with system size. This is a specific case of what is called the Mermin-Wagner theorem in spin systems. Product highlight
KT Transition : Disordered Phases with different correlationsIn the XY model in two dimensions,a second order phase transition is not seen. However,one finds a low temperature disordered phase with a power law correlation(see Correlation function (statistical mechanics)), with a temperature dependent power. The transition from the high temperature disordered phase with the exponential correlation to this low temperature disordered phase with a power law correlation is the Kosterlitz-Thouless transition. Role of VorticesIn the XY model in 2 dimensions, vortices are topologically stable configurations. It is found that the high temperature disordered phase with exponential correlation is a result of the formation of vortices. The temperature at which the KT transition occurs is in fact that at which vortex generation becomes thermodynamically favourable. At temperatures below this, the system has a power law correlation. Informal DescriptionThere is a very elegant thermodynamic argument for the KT transition. The energy of a single vortex is of the form κln(R / a), where κ is a parameter depending upon the system the vortex is in, R is the system size, and a is the radius of the vortex core. We assume R > > a. The number of possible positions of any vortex in the system is approximately (R / a)2. From Boltzmann's law, the entropy is S = 2kBln(R / a), where kB is Boltzmann's constant. Thus, the Helmholtz free energy is
When F > 0, the system is unstable to having a vortex. However when F < 0, the conditions are sufficient for a vortex to be in the system. We define the transition temperature for F = 0. Thus,
Rigorous AnalysisWe have a field φ over the plane which takes on values in S1. For convenience, we work with its universal cover R instead but identify any two values of φ(x) which differs by an integer multiple of 2π. The energy is given by and the Boltzmann factor is exp(-βE). If we take the contour integral Now, It's easy to see that unless When This is nothing other than a Coulomb gas, of course. The scale L contributes nothing but a constant. Let's look at the case with only one vortex of multiplicity one and one vortex of multiplicity -1. At low temperatures, i.e. large β, because of the Boltzmann factor, the vortex-antivortex pair tends to be extremely close to one another. In fact, their separation would be around the cutoff scale. With more vortex-antivortex pairs, we have a collection of vortex-antivortex dipoles. At large temperatures, i.e. small β, the probability distribution swings the other way around and we have a plasma of vortices and antivortices. The phase transition between the two is the Kosterlitz-Thouless phase transition. See also
References
Categories: Statistical mechanics | Lattice models |
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Kosterlitz-Thouless_transition". A list of authors is available in Wikipedia. |





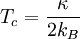 .
.
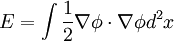
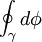 over any closed path γ, we would expect it to be zero if γ is contractible, which is what we would expect for a planar curve. But here is the catch. Assume the XY theory has a UV cutoff which requires some UV completion. Then, we can have punctures in the plane, holes so to speak so that if γ is a closed path which winds once around the puncture,
over any closed path γ, we would expect it to be zero if γ is contractible, which is what we would expect for a planar curve. But here is the catch. Assume the XY theory has a UV cutoff which requires some UV completion. Then, we can have punctures in the plane, holes so to speak so that if γ is a closed path which winds once around the puncture, 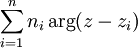 where we have switched to the complex plane coordinates for convenience. The latter term has branch cuts, of course, but since φ is only defined modulo 2π they are unphysical.
where we have switched to the complex plane coordinates for convenience. The latter term has branch cuts, of course, but since φ is only defined modulo 2π they are unphysical.
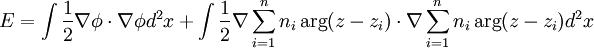
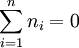 , the second term is positive infinite, making the Boltzmann factor zero which means that we can forget all about it.
, the second term is positive infinite, making the Boltzmann factor zero which means that we can forget all about it.
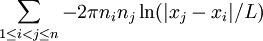 .
.


