To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Mermin-Wagner theorem
In quantum field theory and statistical mechanics, the Mermin-Wagner theorem (also known as Mermin-Wagner-Hohenberg theorem or Coleman theorem) states that continuous symmetries cannot be spontaneously broken at finite temperature in one and two dimensional theories. This is because if such a spontaneous symmetry breaking occurred, then the corresponding Goldstone bosons, being massless, would have an infrared divergent correlation function. Intuitively, this means that long-range fluctuations can be created with little energy cost and since they increase the entropy they are favored. The absence of spontaneous symmetry breaking in one and two dimensional systems was rigorously proved by Coleman in quantum field theory and by Mermin, Wagner and Hohenberg in statistical physics.
Product highlight
IntroductionConsider the free scalar field φ of mass m in two Euclidean dimensions. Its propagator is: For small m, G is a solution to Laplace's equation with a point source: This is because the propagator is the reciprocal of So that the function G has a logarithmic divergence both at small and large r. The interpretation of the divergence is that the field fluctuations cannot stay centered around a mean. If you start at a point where the field has the value 1, the divergence tells you that as you travel far away, the field is arbitrarily far from the starting value. This makes a two dimensional massless scalar field slightly tricky to define mathematically. If you define the field by a monte-carlo simulation, it doesn't stay put, it slides to infinitely large values with time. This happens in one dimension too, when the field is a one dimensional scalar field, a random walk in time. A random walk also moves arbitrarily far from its starting point, so that a one-dimensional or two-dimensional scalar does not have a well defined average value. If the field is an angle, θ, as it is in the mexican hat model where the complex field A = Reiθ has an expectation value but is free to slide in the θ direction, the angle θ will be random at large distances. This is the Mermin Wagner theorem: There is no spontaneous breaking of a continuous symmetry in two dimensions. Kosterlitz-Thouless transitionMain article: Kosterlitz-Thouless transition Another example is the XY model. The Mermin-Wagner theorem prevents any spontaneous symmetry breaking of the XY U(1) symmetry. However, it does not prevent the existence of an ordered phase. Heisenberg modelWe will consider the Heisenberg model in d dimensions, that is a system of n-component spins The name of this model comes from its rotational symmetry. Let us consider the low temperature behavior of this system and assume that there exists a spontaneously broken, that is a phase where all spins point in the same direction, e.g. along the x-axis. Then the O(n) rotational symmetry of the system is spontaneously broken, or rather reduced to the O(n − 1) symmetry under rotations around this direction. We can parametrize the field in terms of independent fluctuations σα around this direction as follows with whence Ignoring the irrelevant constant term H0 = − JNd and passing to the continuum limit, given that we are interested in the low temperature phase where long-wavelength fluctuations dominate, we get The field fluctuations σα are called spin waves and can be recognized as Goldstone bosons. Indeed, they are n-1 in number and they have zero mass since there is no mass term in the Hamiltonian. To find if this hypothetical phase really exists we have to check if our assumption is self-consistent, that is if the expectation value of the magnetization, calculated in this framework, is finite as assumed. To this end we need to calculate the first order correction to the magnetization due to the fluctuations. This is the procedure followed in the derivation of the well-known Ginzburg criterion. The model is Gaussian to first order and so the momentum space correlation function is proportional to 1 / k2. Thus the real space two-point correlation function for each of these modes is where a is the lattice spacing. The average magnetization is The integral above is proportional to and so it is finite for d>2, but appears to be logarithmically divergent for We thus conclude that for
The result can also be extended to other geometries, such as Heisenberg films with an arbitrary number of layers, as well as to other lattice systems (Hubbard model, s-f model). (See ref. [4]) References1. P.C. Hohenberg: "Existence of Long-Range Order in One and Two Dimensions", Phys. Rev. 158, 383 (1967) 2. N.D. Mermin, H. Wagner: "Absence of Ferromagnetism or Antiferromagnetism in One- or Two-Dimensional Isotropic Heisenberg Models", Phys. Rev. Lett. 17, 1133–1136 (1966) 3. Sidney Coleman: "There are no Goldstone bosons in two dimensions", Commun. Math. Phys. 31, 259 (1973) 4. Axel Gelfert, Wolfgang Nolting: "The absence of finite-temperature phase transitions in low-dimensional many-body models: a survey and new results", J. Phys.: Condens. Matter 13, R505-R524 (2001) |
|||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Mermin-Wagner_theorem". A list of authors is available in Wikipedia. |





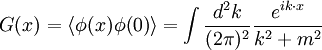
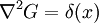
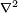 in k space. To use Gauss's law, define the electric field analog to be
in k space. To use Gauss's law, define the electric field analog to be 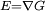 . The divergence of the electric field is zero. In two dimensions, using a large Gaussian ring:
. The divergence of the electric field is zero. In two dimensions, using a large Gaussian ring:
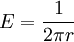
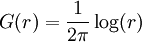
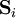 of unit length
of unit length 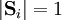 , located at the sites of a d-dimensional square lattice, with nearest neighbor coupling J. Thus the Hamiltonian is
, located at the sites of a d-dimensional square lattice, with nearest neighbor coupling J. Thus the Hamiltonian is
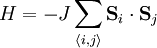
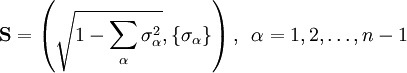
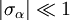 and Taylor expand the resulting Hamiltonian. We have
and Taylor expand the resulting Hamiltonian. We have
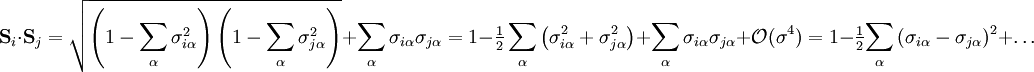
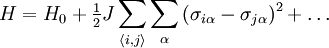
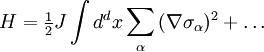
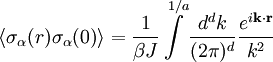
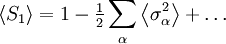 and the first order correction can now easily be calculated
and the first order correction can now easily be calculated
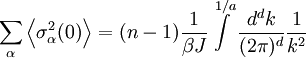
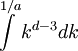
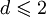 . However, this is really an artifact of the linear approximation. In a more careful treatment, the average magnetization is zero.
. However, this is really an artifact of the linear approximation. In a more careful treatment, the average magnetization is zero.


