To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Spin waveSpin waves are propagating disturbances in the ordering of magnetic materials. These low-lying collective excitations occur in magnetic lattices with continuous symmetry. From the equivalent quasiparticle point of view, spin waves are known as magnons, which are boson modes of the spin lattice that correspond roughly to the phonon excitations of the nuclear lattice. As temperature is increased, the thermal excitation of spin waves reduces a ferromagnet's spontaneous magnetization. The energies of spin waves are typically only μeV in keeping with typical Curie points at room temperature and below. The discussion of spin waves in antiferromagnets is beyond the scope of this article. Product highlight
Theory
The simplest way of understanding spin waves is to consider the Hamiltonian
where J is the exchange energy, the operators S represent the spins at Bravais lattice points, g is the gyromagnetic ratio, μB is the Bohr magneton and
resulting in
where z has been taken as the direction of the magnetic field. The spin-lowering operator S − annihilates the state with a zero projection of spin along the z-axis, while the spin-raising operator S + annihilates the ground state with maximum spin projection along the z-axis. Since
where N is the total number of Bravais lattice sites. The proposition that the ground state is an eigenstate of the Hamiltonian is confirmed. One might guess that the first excited state of the Hamiltonian has one randomly selected spin at position i rotated so that In this model the magnetization
where γ is the gyromagnetic ratio and λ is the damping constant. The cross-products in this forbidding-looking equation show that the propagation of spin waves is governed by the torques generated by internal and external fields. The first term describes the precession of the magnetization under the influence of the applied field, while the second describes how the magnetization vector spirals in towards the field direction as time progresses. In metals the damping forces described by the constant λ are in many cases dominated by the eddy currents. One important difference between phonons and magnons lies in their dispersion relations. The dispersion relation for phonons is to first order linear in wavevector k: ω = ck, where ω is frequency, and c is the velocity of sound. Magnons have a parabolic dispersion relation: ω = Ak2 where the parameter A represents a "spin stiffness." The k2 form is the first term of a Taylor expansion of a cosine term in the energy expression originating from the Experimental observationSpin waves are observed through four experimental methods: inelastic neutron scattering, inelastic light scattering (Brillouin scattering, Raman scattering and inelastic X-ray scattering), inelastic electron scattering (spin-resolved electron energy loss spectroscopy) and spin-wave resonance, also known as ferromagnetic resonance. In the first method the energy loss of a beam of neutrons that excite a magnon is measured, typically as a function of scattering vector (or equivalently momentum transfer), temperature and external magnetic field. Inelastic neutron scattering measurements can determine the dispersion curve for magnons just as they can for phonons. Important inelastic neutron scattering facilities are present at the ISIS neutron source in Oxfordshire, UK, the Institut Laue-Langevin in Grenoble, France, the High Flux Isotope Reactor at Oak Ridge National Laboratory in Tennessee, USA, and at the National Institute of Standards and Technology in Maryland, USA. Brillouin scattering similarly measures the energy loss of photons (usually at a convenient visible wavelength) reflected from or transmitted through a magnetic material. Brillouin spectroscopy is similar to the more widely known Raman scattering but probes a lower energy and has a higher energy resolution in order to be able to detect the meV energy of magnons. Ferromagnetic (or antiferromagnetic) resonance instead measures the absorption of microwaves, incident on a magnetic material, by spin waves, typically as a function of angle, temperature and applied field. Ferromagnetic resonance is a convenient laboratory method for determining the effect of magnetocrystalline anisotropy on the dispersion of spin waves. Very recently, one group in Max Planck Institute for Microstructurephysics in Halle Germany proved that by using spin polarized electron energy loss spectroscopy (SPEELS), very high energy surface magnons can be exited. This technique allows people first time to probe the magnons and its dispersion in the ultrathin magnetical system. The first experiment was successful done in 5 ML Fe film by SPEELS, the signature of magnons were revealed. Later, with momentum resolution, magnon dispersion and full peak was explored in 8 ML fcc Co film on Cu(001) and 8 ML hcp Co on W(110), respectively. Those magnons are obtained up to the SBZ at the energy range about few hundreds meV. Practical SignificanceWhen magnetoelectronic devices are operated at high frequencies, the generation of spin waves can be an important energy loss mechanism. Spin wave generation limits the linewidths and therefore the quality factors Q of ferrites components used in microwave devices. The reciprocal of the lowest frequency of the characteristic spin waves of a magnetic material gives a time scale for the switching of a device based on that material. See alsoReferences1. List of labs performing Brillouin scattering measurements. 5. M.Plihal, D.L.Mills, and J.Kirschner, " Spin wave signature in the spin polarized electron energy loss spectrum in ultrathin Fe film: theory and experiment" Phys. Rev. Lett. , 82, 2579,(1999) 6. R.Vollmer, M.Etzkorn, P.S.Anil Kumar, H.lbach, and J.Kirschner, "Spin polarized electron energy loss spectroscopy of high energy, large wave vector spin waves in fcc Co films on Cu(001)" Phys. Rev. Lett. , 91, 147201,(2003) 7. A.T.Costa, R. B. Muniz and D. L. Mills, "Theory of spin waves in ultrathin ferromagnetic films: the case of Cu on Cu(100)" , Phys. Rev. B 69, 064413 (2004) 8. A.T.Costa, R. B. Muniz and D. L. Mills, "Theory of large wave-vector spin waves in ferromagnetic films: sensitivity to electronic structure", Phys. Rev. B 70, 54406 (2004) |
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Spin_wave". A list of authors is available in Wikipedia. |





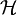 for the Heisenberg ferromagnet:
for the Heisenberg ferromagnet:
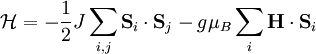
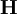 is the internal field which includes the external field plus any "molecular" field. For a ferromagnet
is the internal field which includes the external field plus any "molecular" field. For a ferromagnet  is that in which all spins are aligned parallel with the field
is that in which all spins are aligned parallel with the field 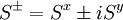
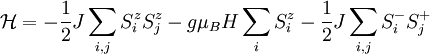
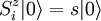 for the maximally aligned state, we find
for the maximally aligned state, we find
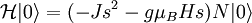
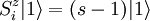 , but in fact this arrangement of spins is not an eigenstate. The reason is that such a state is transformed by the spin raising and lowering operators. The operator
, but in fact this arrangement of spins is not an eigenstate. The reason is that such a state is transformed by the spin raising and lowering operators. The operator 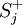 will increase the z-projection of the spin at position
will increase the z-projection of the spin at position 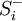 will lower the z-projection of the spin at position
will lower the z-projection of the spin at position 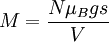 where
where 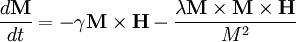
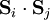 dot-product.The underlying reason for the difference in dispersion relation is that ferromagnets violate
dot-product.The underlying reason for the difference in dispersion relation is that ferromagnets violate 

