To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Quantum vortexA quantum vortex is a topological defect exhibited in superfluids and superconductors. The existence of these quantum vortices were independently predicted by Richard Feynman and Alexei Alexeyevich Abrikosov in the 1950s. They were later observed experimentally in Type-II superconductors, liquid helium, and atomic gases (see Bose-Einstein condensate). A quantum vortex in a superfluid is different than one in a superconductor. The key similarity is that they are both topological defects, and they are both quantized. In addition, the make up of each quantum vortex is neither superfluid nor superconductor, for each system. In a superfluid, a quantum vortex "carries" the angular momentum, thus allowing the superfluid to rotate; in a superconductor, the vortex carries the magnetic flux. Product highlight
Vortex in a superfluidIn a superfluid, a quantum vortex is a hole with the superfluid circulating around the vortex; the inside of the vortex may contain excited particles, air, vacuum, etc. The thickness of the vortex depends upon the chemical make-up of the superfluid; in liquid helium, the thickness is on the order of a few Angstroms. A superfluid has the special property of having phase, given by the wavefunction, and the velocity of the superfluid is proportional to the gradient of the phase. The circulation around any closed loop in the superfluid is zero, if the region enclosed is simply connected. The superfluid is deemed irrotational. However, if the enclosed region actually contains a smaller region that is an absence of superfluid, for example a rod through the superfluid or a vortex, then the circulation is, where Vortex in a superconductorA principal property of superconductors is that they expel magnetic fields; this is called the Meissner effect. If the magnetic field becomes sufficiently strong, one scenerio is for the superconductive state to be "killed". However, in some cases, it may be energertically favorable for the superconductor to form a quantum vortex, which carries a quantized amount of magnetic flux through the superconductor. Meanwhile, the superconductive state prevails in the regions around the vortex. A superconductor that is capable of carrying a vortex is called a type-II superconductor. Over some enclosed area S, the magnetic flux is
Substituting a result of London's second equation:
where n_s, m, and e_s are the number density, mass and charge of the Cooper pairs. If the region, S, is large enough so that
see also
References
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Quantum_vortex". A list of authors is available in Wikipedia. |





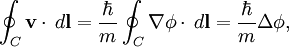
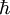 is Planck's constant divided by
is Planck's constant divided by 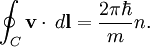
 .
.
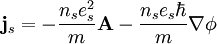 , we find
, we find
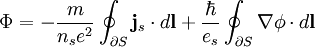 ,
,
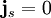 along
along 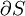 , then
, then
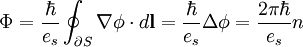 .
.


