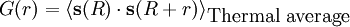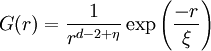Correlation function (statistical mechanics)

The correlation function in statistical mechanics is measure of the order in a system. It tells us how microscopic variables at different positions are correlated. In a spin system, it is the thermal average of the scalar product of the spins at two lattice points over all possible orderings. The correlation function is hence,

$G (r) = \langle \mathbf{s}(R) \cdot \mathbf{s}(R+r)\rangle_{\mbox{Thermal average}}$

Additional recommended knowledge

Daily Visual Balance Check

How to quickly check pipettes?

Essential Laboratory Skills Guide

Even in a disordered phase,spins at different positions are correlated. The alignment that would naturally arise as a result of the interaction between spins is destroyed by thermal effects. At high temperatures one sees an exponential correlation with the correlation function being given by,

$G (r) = \frac{1}{r^{d-2+\eta}}\exp{\left(\frac{-r}{\xi}\right)}$

where $ξ$ is what is called the correlation length, r is the distance between spins and d is the dimension of the system. As the temperature is lowered, thermal disordering is lowered and the correlation length increases. In second order phase transitions, the correlation length diverges at the critical point, leading to a power law correlation, that is responsible for scaling, seen in these transitions. The power in the power law is independent of temperature. It is in fact universal, i.e found to be the same in a wide variety of systems.

One very important correlation function is the radial distribution function which is seen often in statistical mechanics.

Category: Statistical mechanics