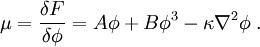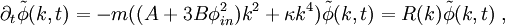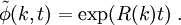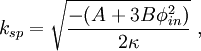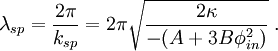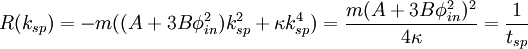To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Spinodal decompositionSpinodal decomposition is a method by which a mixture of two or more materials can separate into distinct regions with different material concentrations. This method differs from nucleation in that phase separation due to spinodal decomposition occurs throughout the material, and not just at nucleation sites. Product highlightSpinodal region of the phase diagramPhase separation occurs whenever a material transitions into the unstable region of the phase diagram. The boundary of the unstable region, sometimes referred to as the binodal, is found by performing a common tangent construction of the free-energy diagram. Inside the binodal is a region called the spinodal, which is found by determining where the curvature of the free-energy curve is negative. The binodal and spinodal meet at the critical point. It is when a material is moved into the spinodal region of the phase diagram that spinodal decomposition can occur.[1] To reach the spinodal region of the phase diagram, a transition must take the material through the binodal region or the critical point. Often phase separation will occur via nucleation during this transition, and spinodal decomposition will not be observed. To observe spinodal decomposition, a very fast transition, often called a quench, is required to move from the stable to the spinodally unstable region of the phase diagram. The dynamics of spinodal decompositionIn the spinodal region of the phase diagram, the free-energy can be lowered by allowing the components to separate, thus increasing the relative concentration of a component material in a particular region of the material. The concentration will continue to increase until the material reaches the stable part of the phase diagram. Very large regions of material will change their concentration slowly due to the amount of material which must be moved. Very small regions will shrink away due to the energy cost in maintaining an interface between two dissimilar component materials. To initiate a homogeneous quench a control parameter, such as temperature, is abruptly and globally changed. For a binary mixture of A-type and B-type materials, the Landau free-energy is a good approximation of the free-energy near the critical point and is often used to study homogeneous quenches. The mixture concentration φ = ρA − ρB is the density difference of the mixture components, the control parameters which determine the stability of the mixture are A and B, and the interfacial energy cost is determined by κ. Diffusive motion often dominates at the length-scale of spinodal decomposition. The equation of motion for a diffusive system is where m is the diffusive mobility, ξ(x) is some random noise such that We see that if A < 0, small fluctuations around φ = 0 have a negative effective diffusive mobility and will grow rather than shrink. To understand the growth dynamics, we disregard the fluctuating currents due to ξ, linearize the equation of motion around φ = φin and perform a Fourier transform into k-space. This leads to which has an exponential growth solution: Since the growth rate R(k) is exponential, the fastest growing angular wavenumber will quickly dominate the morphology. We now see that spinodal decomposition results in domains of the characteristic length scale called the spinodal length: The growth rate of the fastest growing angular wave number is where tsp is known as the spinodal time. The spinodal length and spinodal time can be used to nondimensionalize the equation of motion, resulting in universal scaling for spinodal decomposition. References
Categories: Condensed matter physics | Thermodynamics | Materials science |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Spinodal_decomposition". A list of authors is available in Wikipedia. |





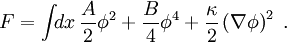
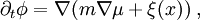
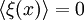 , and the chemical potential
, and the chemical potential