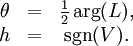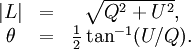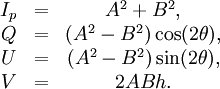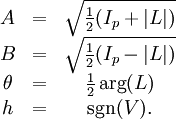To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Stokes parametersThe Stokes parameters are a set of values that describe the polarization state of electromagnetic radiation (including visible light). They were introduced by George Gabriel Stokes in 1852, as a mathematically convenient alternative to the more common description of incoherent or partially polarized radiation in terms of its total intensity (I), (fractional) degree of polarization (p), and the shape parameters of the polarization ellipse. The relationship of the Stokes parameters to intensity and polarization ellipse parameters is shown in the equations and figure below. Here Ip, 2ψ and 2χ are the spherical coordinates of the polarization state in the three-dimensional space of the last three Stokes parameters. Note the factor of two before ψ represents the fact that any polarization ellipse is indistinguishable from one rotated by 180°, while the factor of two before χ indicates that an ellipse is indistinguishable from one with the semi-axis lengths swapped accompanied by a 90° rotation. The four Stokes parameters are sometimes denoted I, Q, U and V, respectively. If given the Stokes parameters one can solve for the spherical coordinates with the following equations: Product highlight
Stokes vectorsThe Stokes parameters are often combined into a vector, known as the Stokes vector: The Stokes vector spans the space of unpolarized, partially polarized, and fully polarized light. For comparison, the Jones vector only spans the space of fully polarized light, but is more useful for problems involving coherent light. The four Stokes parameters do not form a preferred basis of the space, but rather were chosen because they can be easily measured or calculated. The effect of an optical system on the polarization of light can be determined by constructing the Stokes vector for the input light and applying Mueller calculus, to obtain the Stokes vector of the light leaving the system. ExamplesBelow are shown some Stokes vectors for common states of polarization of light.
Alternate ExplanationA monochromatic plane wave is specified by its propagation vector, One way to describe polarization is by giving the semi-major and semi-minor axes of the polarization ellipse, its orientation, and the sense of rotation (See the above figure). The Stokes parameters I, Q, U, and V, provide an alternative description of the polarization state which is experimentally convenient because each parameter corresponds to a sum or difference of measurable intensities. The next figure shows examples of the Stokes parameters in degenerate states. DefinitionsThe Stokes parameters are defined by where the subscripts refer to three bases: the standard Cartesian basis ( Representations in fixed basesIn a fixed ( while for and for PropertiesFor purely monochromatic coherent radiation, one can show that whereas for the whole (non-coherent) beam radiation, the Stokes parameters are defined as averaged quantities, and the previous equation becomes an inequality[1]: However, we can define a total polarization intensity Ip, so that where Ip / I is the total polarization fraction. Let us define the complex intensity of linear polarization to be Under a rotation With these properties, the Stokes parameters may be thought of as constituting three generalized intensities: where I is the total intensity, | V | is the intensity of circular polarization, and | L | is the intensity of linear polarization. The total intensity of polarization is Since Q = Re(L) and U = Im(L), we have Relation to the polarization ellipseIn terms of the parameters of the polarization ellipse, the Stokes parameters are Inverting the previous equation gives See alsoReferences
Categories: Polarization | Radiometry |
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Stokes_parameters". A list of authors is available in Wikipedia. |


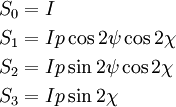
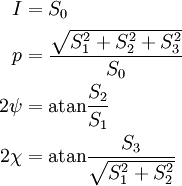



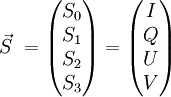
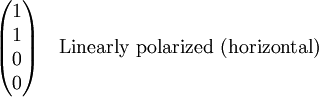
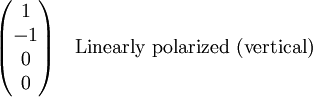
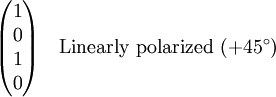
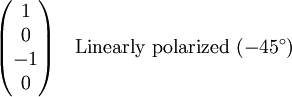


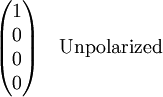
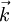 , and the complex amplitudes of the electric field,
, and the complex amplitudes of the electric field, 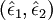 . Alternatively, one may specify the propagation vector, the phase,
. Alternatively, one may specify the propagation vector, the phase, 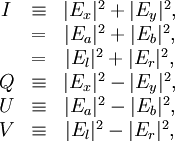
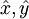 ), a Cartesian basis rotated by 45° (
), a Cartesian basis rotated by 45° (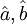 ), and a circular basis (
), and a circular basis (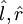 ). The circular basis is defined so that
). The circular basis is defined so that 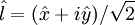 . The next figure shows how the signs of the Stokes parameters are determined by the helicity and the orientation of the semi-major axis of the polarization ellipse.
. The next figure shows how the signs of the Stokes parameters are determined by the helicity and the orientation of the semi-major axis of the polarization ellipse.
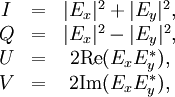
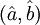 , they are
, they are
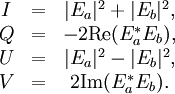
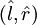 , they are
, they are
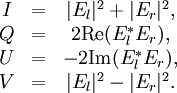
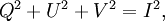
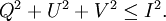
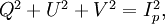
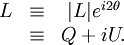
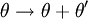 of the polarization ellipse, it can be shown that
of the polarization ellipse, it can be shown that 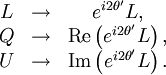
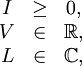
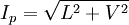 , and the orientation and sense of rotation are given by
, and the orientation and sense of rotation are given by