To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Jones calculusIn optics one can describe polarization using the Jones calculus, invented by R. C. Jones in 1941. Polarized light is represented by a Jones vector, and linear optical elements are represented by Jones matrices. When light crosses an optical element the resulting polarization of the emerging light is found by taking the product of the Jones matrix of the optical element and the Jones vector of the incident light. Product highlightThe Jones vector for polarized light is defined by
The following table gives examples of normalized Jones vectors. (i is the imaginary unit,
The following table gives examples of Jones matrices.
If an optical element is rotated about the optical axis by angle θ, the Jones matrix for the rotated element, M(θ), is constructed from the matrix for the unrotated element, M, by the transformation
Note that Jones calculus is only applicable to light that is already fully polarized. Light which is unpolarized, partially polarized, or incoherent must be treated using Mueller calculus. References
See also |
||||||||||||||||||||||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Jones_calculus". A list of authors is available in Wikipedia. |





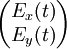 , where
, where 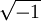 .)
.)
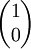
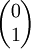
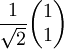
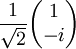
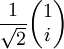
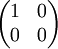
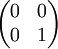
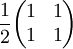
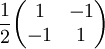
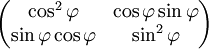
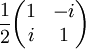
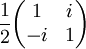
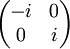
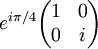
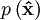 ,
,
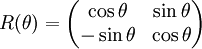 .
.


