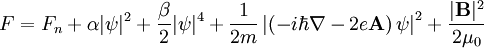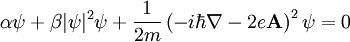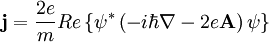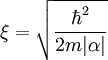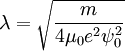To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Ginzburg-Landau theoryIn physics, Ginzburg-Landau theory is a mathematical theory used to model superconductivity. It does not purport to explain the microscopic mechanisms giving rise to superconductivity. Instead, it examines the macroscopic properties of a superconductor with the aid of general thermodynamic arguments. Product highlightBased on Landau's previously-established theory of second-order phase transitions, Landau and Ginzburg argued that the free energy F of a superconductor near the superconducting transition can be expressed in terms of a complex order parameter ψ, which describes how deep into the superconducting phase the system is. The free energy has the form where Fn is the free energy in the normal phase, α and β are phenomenological parameters, m is an effective mass, A is the electromagnetic vector potential, and B (=rot A) is the magnetic induction. By minimizing the free energy with respect to fluctuations in the order parameter and the vector potential, one arrives at the Ginzburg-Landau equations where j denotes the electrical current density and Re the real part. The first equation, which bears interesting similarities to the time-independent Schrödinger equation, determines the order parameter ψ based on the applied magnetic field. The second equation then provides the superconducting current. The Ginzburg-Landau equations produce many interesting and valid results. Perhaps the most important of these is its prediction of the existence of two characteristic lengths in a superconductor. The first is a coherence length ξ, given by which describes the size of thermodynamic fluctuations in the superconducting phase. The second is the penetration depth λ, given by where ψ0 is the equilibrium value of the order parameter in the absence of an electromagnetic field. The penetration depth describes the depth to which an external magnetic field can penetrate the superconductor. The ratio κ = λ/ξ is known as the Ginzburg-Landau Parameter. It has been shown that Type I superconductors are those with κ < 1/√2, and Type II superconductors those with κ > 1/√2. For Type II superconductors, the phase transition from the normal state is of second order, for Type I superconductors it is of first order. This is proved by deriving a dual Ginzburg-Landau theory for the superconductor (see Chapter 13 of the third textbook below). The most important finding from Ginzburg-Landau theory was made by Alexei Abrikosov in 1957. In a type-II superconductor in a high magnetic field - the field penetrates in quantized tubes of flux, which are most commonly arranged in a hexagonal arrangement. This theory arises as the scaling limit of the XY model. The importance of the theory is also enhanced by a certain similarity with the Higgs mechanism in High-energy physics. see alsoReferencesPapers
Books
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Ginzburg-Landau_theory". A list of authors is available in Wikipedia. |