To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Compressibility equationIn statistical mechanics and thermodynamics the compressibility equation refers to an equation which relates the isothermal compressibility (and indirect the pressure) to the structure of the liquid. It reads: Product highlight
where ρ is the number density, g(r) is the radial distribution function and Using the Fourier representation of the Ornstein-Zernike equation the compressibility equation (1) can be rewritten in the form:
where h(r) and c(r) are the indirect and direct correlation functions respectively. The compressibility equation is one of the many integral equations in statistical mechanics. References
Categories: Statistical mechanics | Thermodynamics |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Compressibility_equation". A list of authors is available in Wikipedia. |





![kT\left(\frac{\partial \rho}{\partial p}\right)=1+\rho \int d r [g(r)-1]](images/math/7/3/9/7398478c87fd42d409c1fda60f0c2b07.png) (1)
(1)
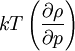 is the isothermal
is the isothermal 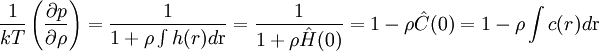 (2)
(2)


