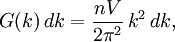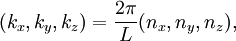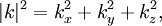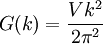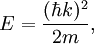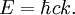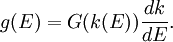Density of states

In statistical and condensed matter physics, Density of states (DOS) is a property that quantifies how closely packed energy levels are in a quantum-mechanical system. It is usually denoted with one of the symbols g, ρ, n, or N. It is a function g(E) of the internal energy E, such that the expression g(E) dE represents the number of states with energies between E and E+dE. It can also be written as a function of the angular frequency ω, which is proportional to the energy. The density of states is used extensively in condensed-matter physics, where it can refer to electron, photon, or phonon energy levels in a crystalline solid. In crystalline solids, there are often energy ranges where the density of electron states is zero, which means that the electrons cannot be excited to these energies. The density of states also occurs in Fermi's golden rule, which describes how fast quantum-mechanical transitions occur in the presence of a perturbation.

Additional recommended knowledge

What is the Correct Way to Check Repeatability in Balances?

Daily Sensitivity Test

Safe Weighing Range Ensures Accurate Results

In a three-dimensional system, the density of states in reciprocal space (k-space) is

where V is the volume and n the number of branches that exist for a single value of k. These branches are for example the spin-up and spin-down states for electrons, the polarizations of photons, and longitudinal or transversal modes for phonons.

Since in (crystalline) materials, the number of states scales linearly with the volume, a different definition of the density of states is sometimes used, in which g(E) or g(k) is the number of states per unit of energy (wavevector) and per unit volume or per lattice unit cell.

Crystalline materials

In a crystalline material, where quantum-mechanical states can be described in terms of their wavevector k, the density of states as a function of k is not dependent on the material properties. From the periodic boundary condition it follows that in an arbitrary volume V = L³, only k vectors are allowed satisfying

where n_i are arbitrary positive or negative integers. Using

it can be derived that the number of states G(k) dk between k and k+dk is

for a single branch.

To calculate the density of energy states g(E), knowledge of the relationship between k and E is required. For example, for an electron in vacuum,

and for a photon in vacuum,

In solids, the relation between E and k is generally very complex and dependent on the material. If the relation is known, the expression for the density of states is

The above relation is only meaningful if the energy only depends on the magnitude | k | of the vector k.

Photonic crystals

Main article: Photonic crystal

A photonic crystal is a structure that has a periodic structure on the scale of the wavelength of light, rather than on the scale of atomic dimensions. In a photonic crystal, the density of photon states is zero for photons propagating in certain directions, and sometimes even in any direction. The latter has the interesting consequence that an excited atom or molecule embedded in such a photonic crystal cannot make a transition to the ground state by radiating a photon, while it would make this transition if it had been in vacuum or an ordinary material.

See also

• van Hove singularity