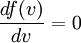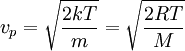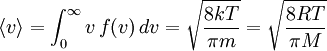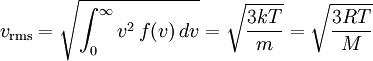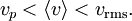To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Maxwell–Boltzmann distribution
The distribution can be thought of as the magnitude of a 3-dimensional vector if its components are distributed as a normal distribution with standard deviation a. If Xi are distributed as X˜N(0,a2), then is distributed as a Maxwell–Boltzmann distribution with parameter a. Product highlight
PropertiesThe Maxwell-Boltzmann distribution curve shows how particle velocities are distributed in an average sample of particles. At any given temperature very few particles will possess very low or very high energy (most will possess an energy level somewhere in between the two extremes); this is called the mean energy. The activation energy barrier needs to be overcome if a reaction is to take place. If we increase the number of particles, i.e. increase the concentration of reactants, we produce more particles with energy greater than the activation energy (see collision theory). The Maxwell–Boltzmann distribution with a = 1 is equivalent to the chi distribution with three degrees of freedom. Additionally, if Z is distributed as a Maxwell–Boltzmann distribution with parameter a, then will be distributed as a chi distribution with three degrees of freedom. The root-mean-square of a Maxwell–Boltzmann distribution is Physical applications of the Maxwell–Boltzmann distributionThe Maxwell–Boltzmann distribution forms the basis of the kinetic theory of gases, which explains many fundamental gas properties, including pressure and diffusion. The Maxwell–Boltzmann distribution is usually thought of as the distribution of molecular speeds in a gas, but it can also refer to the distribution of velocities, momenta, and magnitude of the momenta of the molecules, each of which will have a different probability distribution function, all of which are related. The Maxwell–Boltzmann distribution can be derived using statistical mechanics (see Maxwell–Boltzmann statistics). It corresponds to the most probable speed distribution in a collisionally-dominated system consisting of a large number of non-interacting particles in which quantum effects are negligible. Since interactions between the molecules in a gas are generally quite small, the Maxwell-Boltzmann distribution provides a very good approximation of the conditions in a gas. There are many cases (such as elastic collisions) where these conditions do not apply. For example, the physics of the ionosphere and space plasmas where recombination and collisional excitation (i.e. radiative processes) are important: especially for electrons. If you applied the Maxwell distribution and its assumptions here, you would get the wrong numbers, and miss the basic physics of the problem. Another example where applying the Maxwell-Boltzmann Distribution would give incorrect results is in cases where the quantum thermal wavelength of the gas is not small compared to the distance between particles. There, the theory would fail to account for significant quantum effects. Also, as it is based on nonrelativistic assumptions, the Maxwell-Boltzmann distribution does not predict zero probability for molecular velocities in excess of the speed of light. The original derivation by Maxwell assumed all three directions would behave in the same fashion, but a later derivation by Boltzmann dropped this assumption using kinetic theory. The Maxwell–Boltzmann distribution can now most readily be derived from the Boltzmann distribution for energies: where Ni is the number of molecules at equilibrium temperature T, in a state i which has energy Ei and degeneracy gi, N is the total number of molecules in the system and k is the Boltzmann constant. (Note that sometimes the above equation is written without the degeneracy factor gi. In this case the index i will specify an individual state, rather than a set of gi states having the same energy Ei.) Because velocity and speed are related to energy, Equation 1 can be used to derive relationships between temperature and the speeds of molecules in a gas. The denominator in this equation is known as the canonical partition function. Distribution of the momentum vectorWhat follows is a derivation wildly different from the derivation described by James Clerk Maxwell and later described with fewer assumptions by Ludwig Boltzmann. Instead it is close to Boltzmann's later approach of 1877. For the case of an "ideal gas" consisting of non-interacting atoms in the ground state, all energy is in the form of kinetic energy. The relationship between kinetic energy and momentum for massive particles is where p² is the square of the momentum vector p = [px, py, pz]. We may therefore rewrite Equation 1 as: where Z is the partition function, corresponding to the denominator in Equation 1. Here m is the molecular mass of the gas, T is the thermodynamic temperature and k is the Boltzmann constant. This distribution of Ni/N is proportional to the probability density function fp for finding a molecule with these values of momentum components, so: The normalizing constant c, can be determined by recognizing that the probability of a molecule having any momentum must be 1. Therefore the integral of equation 4 over all px, py, and pz must be 1. It can be shown that: Substituting Equation 5 into Equation 4 gives: The distribution is seen to be the product of three independent normally distributed variables px py, and pz, with variance mkT. Additionally, it can be seen that the magnitude of momentum will be distributed as a Maxwell–Boltzmann distribution, with Distribution of the energyUsing p² = 2mE we get the energy distribution: Since the energy is proportional to the sum of the squares of the three normally distributed momentum components, this distribution is a chi-square distribution with three degrees of freedom: where The Maxwell–Boltzmann distribution can also be obtained by considering the gas to be a quantum gas. Distribution of the velocity vectorRecognizing that the velocity probability density fv is proportional to the momentum probability density function by and using p = mv we get which is the Maxwell–Boltzmann velocity distribution. The probability of finding a particle with velocity in the infinitesimal element [dvx, dvy, dvz] about velocity v = [vx, vy, vz] is Like the momentum, this distribution is seen to be the product of three independent normally distributed variables vx vy, and vz, but with variance kT / m. It can also be seen that the Maxwell–Boltzmann velocity distribution for the vector velocity [vx, vy, vz] is the product of the distributions for each of the three directions: where the distribution for a single direction is This distribution has the form of a normal distribution, with variance Distribution of speeds
Usually, we are more interested in the speeds of molecules rather than their component velocities. The Maxwell-Boltzmann distribution of speeds is written as where speed, v, is defined as Note that the units of f(v) in equation (10) are probability per speed, or just reciprocal speed as in the graph at the right. Since the speed is the square root of the sum of squares of the three independent, normally distributed velocity components, this distribution is a Maxwell–Boltzmann distribution, with We are often more interested in quantities such as the average speed of the particles rather than the actual distribution. The mean speed, most probable speed (mode), and root-mean-square can be obtained from properties of the Maxwell–Boltzmann distribution. Typical speedsAlthough the above equation gives the distribution of speeds or in other words the fraction of molecules having a particular speed, we are often more interested in quantities such as the average speed of the particles rather than the actual distribution. The most probable speed, vp, is the speed most likely to be possessed by any molecule in the system and corresponds to the maximum value or mode of f(v). To find it, we calculate df/dv, set it to zero and solve for v: which yields: The mean speed is the mathematical average of the speed distribution The root mean square speed, vrms is the square root of the average squared speed: The typical speeds are related as follows: See also
Categories: Gases | Particle statistics | Statistical mechanics |
||||||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Maxwell–Boltzmann_distribution". A list of authors is available in Wikipedia. | ||||||||||||||||


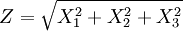



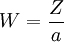
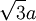 . Since
. Since 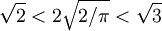 , it follows that the mode is less than the mean, which is always less than the root-mean-square.
, it follows that the mode is less than the mean, which is always less than the root-mean-square.
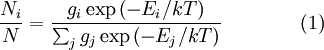
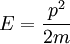
![\frac{N_i}{N} = \frac{1}{Z} \exp \left[ \frac{-(p_x^2 + p_y^2 + p_z^2)}{2mkT} \right] \qquad\qquad (3)](images/math/8/3/8/83837eab6c3309cc6388bd336bcc57af.png)
![f_\mathbf{p} (p_x, p_y, p_z) = \frac{c}{Z} \exp \left[ \frac{-(p_x^2 + p_y^2 + p_z^2)}{2mkT} \right]. \qquad\qquad (4)](images/math/e/5/0/e50bbf12e4b115b842d11ecc64aa9ffd.png)
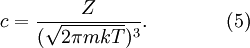
![f_\mathbf{p} (p_x, p_y, p_z) = \sqrt{\left( \frac{1}{2 \pi mkT} \right)^3} \exp \left[ \frac{-(p_x^2 + p_y^2 + p_z^2)}{2mkT} \right]. \qquad\qquad (6)](images/math/1/1/1/1117cd337cb61b7517645c72a923b0da.png)
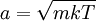 .
.
![f_E\,dE=f_p\left(\frac{dp}{dE}\right)\,dE =2\sqrt{\frac{E}{\pi(kT)^3}}~\exp\left[\frac{-E}{kT}\right]\,dE. \qquad \qquad(7)](images/math/0/b/d/0bd1fa1f40fdbca865f37627c98a7518.png)
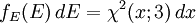
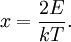
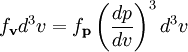
![f_\mathbf{v} (v_x, v_y, v_z) = \sqrt{ \left(\frac{m}{2 \pi kT} \right)^3} \exp \left[ \frac{-m(v_x^2 + v_y^2 + v_z^2)}{2kT} \right], \qquad\qquad (8)](images/math/1/d/a/1da6f8a84540587674440803593f230f.png)
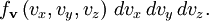
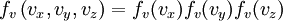
![f_v (v_i) = \sqrt{\frac{m}{2 \pi kT}} \exp \left[ \frac{-mv_i^2}{2kT} \right]. \qquad\qquad (9)](images/math/1/a/b/1abcdfc5e63e2066cb9f8cbfac717053.png)
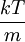 . As expected for a gas at rest, the average velocity in any particular direction is zero.
. As expected for a gas at rest, the average velocity in any particular direction is zero.
![f (v) = 4 \pi \left(\frac{m}{2 \pi kT}\right)^{3/2}\!\!v^2 \exp \left[ \frac{-mv^2}{2kT} \right] \qquad (10)](images/math/8/1/d/81db614753d616c395a65928ac27686c.png)
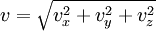
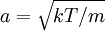 .
.