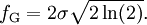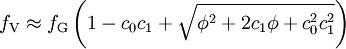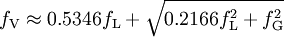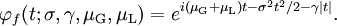To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Voigt profile
In spectroscopy, the Voigt profile is a spectral line profile named after Woldemar Voigt and found in all branches of spectroscopy in which a spectral line is broadened by two types of mechanisms, one of which alone would produce a Gaussian profile (usually, as a result of the Doppler broadening), and the other would produce a Lorentzian profile. All normalized line profiles can be considered to be probability distributions. The Gaussian profile is equivalent to a Gaussian or normal distribution and a Lorentzian profile is equivalent to a Lorentz or Cauchy distribution. Without loss of generality, we can consider only centered profiles which peak at zero. The Voigt profile is then a convolution of a Lorentz profile and a Gaussian profile: where x is frequency from line center, G(x;σ) is the centered Gaussian profile: and L(x;γ) is the centered Lorentzian profile: The defining integral can be evaluated as: where Re[w(z) ] is the real part of the complex error function of z and Product highlight
PropertiesThe Voigt profile is normalized: since it is the convolution of normalized profiles. The Lorentzian profile has no moments (other than the zeroth) and so the moment-generating function for the Cauchy distribution is not defined. It follows that the Voigt profile will not have a moment-generating function either, but the characteristic function for the Cauchy distribution is well defined, as is the characteristic function for the normal distribution. The characteristic function for the (centered) Voigt profile will then be the product of the two: Cumulative distribution functionUsing the above definition for z , the CDF can be found as follows: Substituting the definition of the complex error function yields for the indefinite integral: Which may be solved (see e.g. the Mathematica integrator) to yield: where The width of the Voigt profileThe full width at half maximum (FWHM) of the Voigt profile can be found from the widths of the associated Gaussian and Lorentzian widths. The FWHM of the Gaussian profile is The FWHM of the Lorentzian profile is just fL = 2γ. Define φ = fL / fG. Then the FWHM of the Voigt profile (fV ) can be estimated as: where c0 = 2.0056 and c1 = 1.0593. This estimate will have a standard deviation of error of about 2.4 percent for values of φ between 0 and 10. Note that the above equation will have the proper behavior in the limit of φ = 0 and φ = ∞. A different approximation was given in 1977 by J.J.Olivero and R.L. Longbothum in Empirical fits to the Voigt line width: A brief review, JQSRT 17, P233 with an accuracy of 0.02% The uncentered Voigt profileIf the Gaussian profile is centered at μG and the Lorentzian profile is centered at μL, the convolution will be centered at μG + μL and the characteristic function will then be: The mode and median will then both be located at μG + μL. See also
|
||||||||||||||||||||||||||||||||||||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Voigt_profile". A list of authors is available in Wikipedia. | ||||||||||||||||||||||||||||||||||||||||||||||


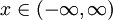
![\frac{\Re[w(z)]}{\sigma\sqrt{2\pi}}, ~~~z=\frac{x+i\gamma}{\sigma\sqrt{2}}](images/math/7/d/6/7d637f96986b0e8356c0125af8a34944.png)
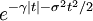
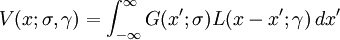
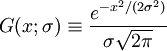
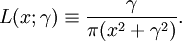
![V(x;\sigma,\gamma)=\frac{\textrm{Re}[w(z)]}{\sigma\sqrt{2 \pi}}](images/math/1/4/a/14a9b10dbecbc80e7f65751e4ab36865.png)
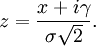



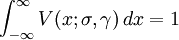
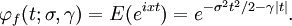
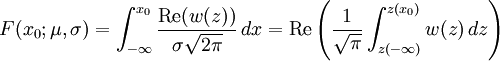
![\frac{1}{\sqrt{\pi}}\int w(z)\,dz =\frac{1}{\sqrt{\pi}} \int e^{-z^2}\left[1-\mathrm{erf}(-iz)\right]\,dz](images/math/6/6/9/669785b036489ca88e1af2d269453cfa.png)
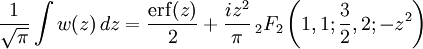
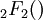 is a hypergeometric function. In order for the function to approach zero as x approaches negative infinity (as the CDF must do), an integration constant of 1/2 must be added. This gives for the CDF:
is a hypergeometric function. In order for the function to approach zero as x approaches negative infinity (as the CDF must do), an integration constant of 1/2 must be added. This gives for the CDF:
![F(x;\mu,\sigma)=\mathrm{Re}\left[\frac{1}{2}+ \frac{\mathrm{erf}(z)}{2} +\frac{iz^2}{\pi}\,_2F_2\left(1,1;\frac{3}{2},2;-z^2\right)\right]](images/math/a/4/2/a42069b18ef999be510d806eaddf5b14.png)