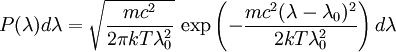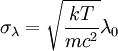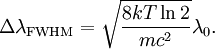To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Doppler broadening
Product highlightThe Doppler profile in wavelength is a normal distribution with a standard deviation of where λ0 is the center wavelength of the profile, c is the speed of light, T is the temperature, k is the Boltzmann constant and m the mass of the atom. For widths that are much smaller than the central wavelength, the Doppler profile in frequency is also a normal distribution with standard deviation where f0 = c / λ0 is the central frequency. The widths are sometimes characterized by the full width at half maximum of the profile (FWHM) which is related to the standard deviation σ by: Derivation of Doppler profileWhen thermal motion causes a particle to move towards the observer, the emitted radiation will be shifted to a higher frequency. Likewise, when the emitter moves away, the frequency will be lowered. For non-relativistic thermal velocities, the Doppler shift in frequency will be: where f is the observed frequency, f0 is the rest frequency, v is the velocity of the emitter towards the observer, and c is the speed of light. Since there is a distribution of speeds both toward and away from the observer in any volume element of gas, the net effect will be to broaden the observed line. The distribution of speeds towards and away from an observer is given by the Maxwell distribution. If P(v)dv is the fraction of particles with velocity component v to v + dv along a line of sight, then: where m is the mass of the emitting particle, T is the temperature and k is the Boltzmann constant. In optics we measure frequency content (as opposed to velocity content), and it is convenient to re-express the distribution in terms of P(f) where P(f)df is the probability of an observed photon having a frequency between f and f + df relative to that stationary observer. The Doppler shift equation can be used to express velocity in terms of the frequency. Using the relationship from probability that P(v)dv = P(f)df, and rearranging terms of the Doppler shift equation above as v = c(f / f0 − 1) such that dv / df = c / f0, we find: We can simplify this expression as:
which we immediately recognize as a Gaussian peak with standard deviation and full width at half maximum We can also consider the above equation in terms of wavelength P(λ) to express the probability of an observed photon having a wavelength between λ to λ + dλ according to the stationary observer. For widths that are small with respect to the central wavelength, we can make the approximation
and furthermore apply the change of variable df = ( − c / λ2)dλ. The Doppler profile in wavelength units is then also a Gaussian: with standard deviation and full width at half maximum Nuclear technology
In a nuclear reactor, this effect reduces the power generated as the reactor temperature increases. When a reactor gets hotter, the accelerated motion of the atoms in the fuel increases the probability of neutron capture by U-238 atoms. When the uranium is heated, its nuclei move more rapidly in random directions, and therefore see and generate a wider range of relative neutron speeds. U-238, which forms the bulk of the uranium in the reactor, is much more likely to absorb fast neutrons.[1] This reduces the number of neutrons available to cause U-235 fission, reducing the power output by the reactor. In some reactor designs, such as the pebble bed reactor, this natural negative feedback places an inherent upper limit on the temperature at which the chain reaction can proceed. Such reactors are said to be "inherently safe" because a reactor failure cannot generate a criticality excursion. It is worth noting, however, that because of decay heat emitted from the decay of fission products, a meltdown is still theoretically possible if the ability to cool the reactor is lost, and thus the reactor design must be designed to prevent loss of coolant accident. AstronomyIn Astronomy, Doppler broadening is one of the explanations for the broadening of spectral lines, and as such gives an indication for the relative temperatures of observed material. There are, however many other factors which can broaden the lines as well. For example high surface gravity (a sign of small stars) leads to high pressure, which in turn leads to Stark-broadening (see Spectral line). |
||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Doppler_broadening". A list of authors is available in Wikipedia. |





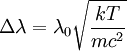
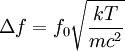
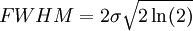
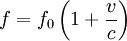
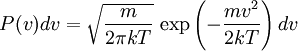
![P(f)df=\left(\frac{c}{f_0}\right)\sqrt{\frac{m}{2\pi kT}}\,\exp\left(-\frac{m\left[c\left(\frac{f}{f_0}-1\right)\right]^2}{2kT}\right)df](images/math/2/a/e/2ae8a4157ef9c41ddc343ac0a97788c3.png)
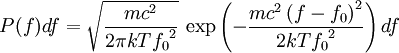 ,
,
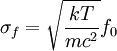
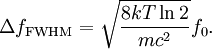
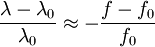 .
.