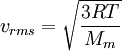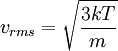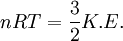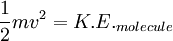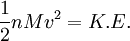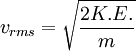Root mean square speed

Root mean square speed is the measure of the speed of particles in a gas that is most convenient for problem solving within the kinetic theory of gases. It is given by the formula

Additional recommended knowledge

Don't let static charges disrupt your weighing accuracy

How to quickly check pipettes?

Safe Weighing Range Ensures Accurate Results

where v_rms is the root mean square speed, M_m is the molar mass of the gas, R is the Molar gas constant, and T is the temperature in Kelvin. This works well for both ideal gases like helium and for molecular gases like diatomic oxygen. This is because despite the larger internal energy in many molecules (compared to that for an atom), 3RT/2 is still the mean translational kinetic energy. This can also be written in terms of the Boltzmann constant (k) as

where m is the mass of the gas.

This can be derived with energy methods:

where K.E. is the kinetic energy.

Given that v² ignores direction, it is logical to assume that the formula can be extended to the entire sample, replacing m with the entire sample's mass, equal to the molar mass times the number of moles, "nM", yielding

Therefore

which is equivalent.

See also

• Boltzmann constant