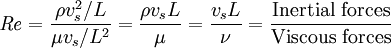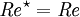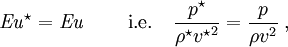To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Reynolds numberIn fluid mechanics, the Reynolds number is the ratio of inertial forces (vsρ) to viscous forces (μ/L) and consequently it quantifies the relative importance of these two types of forces for given flow conditions. It is one of the most important dimensionless numbers in fluid dynamics and is used, usually along with other dimensionless numbers, to provide a criterion for determining dynamic similitude. When two geometrically similar flow patterns, in perhaps different fluids with possibly different flowrates, have the same values for the relevant dimensionless numbers, they are said to be dynamically similar, and will have similar flow geometry. It is also used to identify and predict different flow regimes, such as laminar or turbulent flow. Laminar flow occurs at low Reynolds numbers, where viscous forces are dominant, and is characterized by smooth, constant fluid motion, while turbulent flow, on the other hand, occurs at high Reynolds numbers and is dominated by inertial forces, which tend to produce random eddies, vortices and other flow fluctuations. It is named after Osborne Reynolds (1842–1912), who proposed it in 1883.[1] Product highlight
DefinitionTypically it is given as follows: where vs is the mean fluid velocity in m s-1, L is the characteristic length in m[2], μ is the (absolute) dynamic fluid viscosity in Nsm-2 or Pa s, ν is the kinematic fluid viscosity, defined as ν = μ/ρ, in m2s-1, and ρ is the density of the fluid in kgm-3. For flow in a pipe for instance, the characteristic length is the pipe diameter, if the cross section is circular, or the hydraulic diameter, for a non-circular cross section. For flow over a flat plate, the characteristic length is the length of the plate and the characteristic velocity is the free stream velocity. In a boundary layer over a flat plate the local regime of the flow is determined by the Reynolds number based on the distance measured from the leading edge of the plate. In this case, the transition to turbulent flow occurs at a Reynolds number of the order of 105 or 106. The similarity of flowsIn order for two flows to be similar they must have the same geometry, and have equal Reynolds numbers and Euler numbers. When comparing fluid behaviour at homologous points in a model and a full-scale flow, the following holds: where quantities marked with * concern the flow around the model and the others the real flow. This allows engineers to perform experiments with reduced models in water channels or wind tunnels, and correlate the data to the real flows, saving on costs during experimentation and on lab time. Note that true dynamic similarity may require matching other dimensionless numbers as well, such as the Mach number used in compressible flows, or the Froude number that governs free-surface flows. Some flows involve more dimensionless parameters than can be practically satisfied with the available apparatus and fluids (for example air or water), so one is forced to decide which parameters are most important. For experimental flow modelling to be useful it requires a fair amount of experience and good judgement on the part of the engineer. L, the characteristic length, can be best calculated by finding the squares of frontal length and width and then square rooting the sum. The critical Reynolds numberThe transition between laminar and turbulent flow is often indicated by a critical Reynolds number (Recrit), which depends on the exact flow configuration and must be determined experimentally. Within a certain range around this point there is a region of gradual transition where the flow is neither fully laminar nor fully turbulent, and predictions of fluid behaviour can be difficult. For example, within circular pipes the critical Reynolds number is generally accepted to be 2300, where the Reynolds number is based on the pipe diameter and the mean velocity vs within the pipe, but many engineers will avoid any pipe configuration that falls within the range of Reynolds numbers from about 2000 to 3000 to ensure that the flow is either laminar or turbulent. Reynolds number sets the smallest scales of turbulent motionIn a turbulent flow, there is a range of scales of the time-varying fluid motion. The size of the largest scales of fluid motion (sometime called eddies) are set by the overall geometry of the flow. For instance, in an industrial smoke stack, the largest scales of fluid motion are as big as the diameter of the stack itself. The size of the smallest scales is set by the Reynolds number. As Reynolds number increases, smaller and smaller scales of the flow are visible. In the smoke stack, the smoke may appear to have many very small velocity perturbations or eddies, in addition to large bulky eddies. In this sense, the Reynolds number is an indicator of the range of scales in the flow. The higher the Reynolds number, the greater the range of scales. The largest eddies will always be the same size; the smallest eddies are determined by the Reynolds number. What is the explanation for this phenomenon? A large Reynolds number indicates that viscous forces are not important at large scales of the flow. With a strong predominance of inertial forces over viscous forces, the largest scales of fluid motion are undamped -- there is not enough viscosity to dissipate their motions. The kinetic energy must "cascade" from these large scales to progressively smaller scales until a level is reached for which the scale is small enough for viscosity to become important (that is, viscous forces become of the order of inertial ones). It is at these small scales where the dissipation of energy by viscous action finally takes place. The Reynolds number indicates at what scale this viscous dissipation occurs. Therefore, since the largest eddies are dictated by the flow geometry and the smallest scales are dictated by the viscosity, the Reynolds number can be understood as the ratio of the largest scales of the turbulent motion to the smallest scales. Example of the importance of the Reynolds numberIf an airplane wing needs testing, one can make a scaled down model of the wing and test it in a wind tunnel using the same Reynolds number that the actual airplane is subjected to. If for example the scale model has linear dimensions one quarter of full size, the flow velocity would have to be increased four times to obtain similar flow behaviour. Alternatively, tests could be conducted in a water tank instead of in air. As the kinematic viscosity of water is around 13 times less than that of air at 15 °C, in this case the scale model would need to be about 13 times smaller in all dimensions to maintain the same Reynolds number, assuming the full-scale flow velocity was used. The results of the laboratory model will be similar to those of the actual plane wing results. Thus there is no need to bring a full scale plane into the lab and actually test it. This is an example of "dynamic similarity". Reynolds number is important in the calculation of a body's drag characteristics. A notable example is that of the flow around a cylinder. Above roughly 3×106 Re the drag coefficient drops considerably. This is important when calculating the optimal cruise speeds for low drag (and therefore long range) profiles for airplanes. Reynolds number in physiologyPoiseuille's law on blood circulation in the body is dependent on laminar flow. In turbulent flow the flow rate is proportional to the square root of the pressure gradient, as opposed to its direct proportionality to pressure gradient in laminar flow. Using the Reynold's equation we can see that a large diameter, with rapid flow, where the density of the blood is high tends towards turbulence. Rapid changes in vessel diameter may lead to turbulent flow, for instance when a narrower vessel widens to a larger one. Furthermore, an atheroma may be the cause of turbulent flow, and as such detecting turbulence with a stethoscope may be an indication of such a condition. Typical values of Reynolds number
Onset of turbulent flow ~ 2.3×103-5.0×104 for pipe flow to 106 for boundary layers
See alsoReferences
Categories: Fluid dynamics | Convection |
|||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Reynolds_number". A list of authors is available in Wikipedia. |