To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Dean numberThe Dean number is a dimensionless group in fluid mechanics, which occurs in the study of flow in curved pipes and channels. It is named after the British scientist W. R. Dean, who studied such flows in the 1920's (Dean, 1927, 1928). Product highlightDefinitionThe Dean number is typically denoted by the symbol D, and is defined as where
The Dean number is therefore the product of a Reynolds number (based on axial flow U through a pipe of radius a) and the square root of the length scale ratio a/R. Some authors include an extra numerical factor of 2 in the definition, or call D2 the Dean number. The Dean EquationsThe Dean number appears in the so-called Dean Equations. These are an approximation to the full Navier–Stokes equations for the steady axially uniform flow of a Newtonian fluid in a toroidal pipe, obtained by retaining just the leading order curvature effects (i.e. the leading-order equations for We use an orthogonal coordinates (x,y,z) with corresponding unit vectors In terms of these non-dimensional variables and coordinates, the Dean equations are then where is the convective derivative. The Dean number D is the only parameter left in the system, and encapsulates the leading order curvature effects. Higher-order approximations will involve additional parameters. For weak curvature effects (small D), the Dean equations can be solved as a series expansion in D. The first correction to the leading-order axial Poiseuille flow is a pair of vorticies in the cross-section carrying flow form the inside to the outrside of the bend across the centre and back around the edges. This solution is stable up to a critical Dean number References
|
||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Dean_number". A list of authors is available in Wikipedia. |





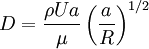
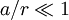 ).
).
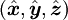 aligned with the centre-line of the pipe at each point. The axial direction is
aligned with the centre-line of the pipe at each point. The axial direction is 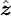 , with
, with 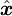 being the normal in the plane of the centre-line, and
being the normal in the plane of the centre-line, and 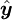 the binormal. For an axial flow driven by a pressure gradient
the binormal. For an axial flow driven by a pressure gradient 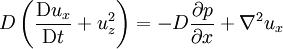
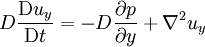
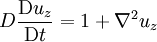
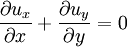
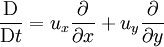
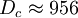 (Dennis & Ng 1982). For larger D, there are multiple solutions, many of which are unstable.
(Dennis & Ng 1982). For larger D, there are multiple solutions, many of which are unstable.


