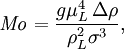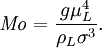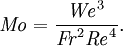My watch list

Morton number

In fluid dynamics, the Morton number ( $M o$ ) is a dimensionless number used together with the Eötvös number to characterize the shape of bubbles or drops. The Morton number is defined as

$\mathit{Mo} = \frac{g \mu_L^4 \, \Delta \rho}{\rho_L^2 \sigma^3},$

Additional recommended knowledge

How to ensure accurate weighing results every day?

where g is the acceleration of gravity, $μ L$ is the viscosity of the surrounding fluid, $ρ L$ the density of the surrounding fluid, $Δρ$ the difference in density of the phases, and $σ$ is the surface tension coefficient. For the case of a bubble with a negligible inner density the Morton number can be simplified to

$\mathit{Mo} = \frac{g\mu_L^4}{\rho_L \sigma^3}.$

The Morton number can also be calculated by using a combination of the Weber number, Froude number and Reynolds number,

$\mathit{Mo} = \frac{\mathit{We}^3}{\mathit{Fr}^2 \mathit{Re}^4}.$

Morton number in theoretical mathematics and computer science

In mathematical number theory and computer science, a Morton number is a single integer value constructed by interleaving the bits or digits of one or more source numbers. This is often useful for constructing a single hash index from a pair (or more) of input numbers. In number theory, Morton numbers are useful in proofs, often in examples which map multiple dimensions to one, or vice versa. For example, an infinite 2D grid of integer coordinates can have a single unique Morton number computed for each coordinate, and those Morton numbers give a one-to-one mapping of the infinite 2D coordinates to a 1D coordinate, proving that the infinite number of integer pairs has the same cardinality as the integers.

Category: Fluid dynamics