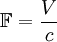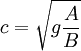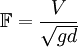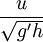Froude number

The Froude number is a dimensionless number comparing inertial and gravitational forces. It may be used to quantify the resistance of an object moving through water, and compare objects of different sizes. Named after William Froude, the Froude number is based on his speed/length ratio.

Additional recommended knowledge

Daily Visual Balance Check

Recognize and detect the effects of electrostatic charges on your balance

Weighing the right way

Origins

  The quantification of the resistance of floating objects is generally credited to Froude, who used a series of scale models to measure the resistance each model offered when towed at a given speed. Froude's observations led him to derive the Wave-Line Theory which first described the resistance of a shape as being a function of the waves caused by varying pressures around the hull as it moves through the water. The Naval Constructor Ferdinand Reech had put forward the concept in 1832 but had not demonstrated how it could be applied to practical problems in ship resistance. Speed/length ratio was originally defined by Froude in his Law of Comparison in 1868 in dimensional terms as:

where:

v = speed in knots

LWL = length of waterline in feet

The term was converted into non-dimensional terms and was given Froude's name in recognition of the work he did. It is sometimes called Reech-Froude number after Ferdinand Reech.

Dimensionless form

The dimensionless Froude number is defined as

where V is an average velocity , and c is the propagation velocity of a shallow water wave. The Froude number is thus the hydrodynamic equivalent to the Mach number.

c is equal to the square root of gravitational acceleration times cross-sectional area divided by free-surface width, i.e.

and so the Froude number can often be simplified to

where d is a depth or length scale.

The Froude number is the reciprocal of the square root of the Richardson number.

Densimetric Froude Number

When used in the context of the Boussinesq approximation the densimetric Froude number is defined as

where g' is the reduced gravity

The densimetric Froude number is usually preferred by modellers who wish to nondimensionalize a speed preference to the Richardson number which is more commonly encountered when considering stratified shear layers. For example, the leading edge of a gravity current moves with a front Froude number of about unity.

Uses

The Froude number is used to compare the wave making resistance between bodies of various sizes and shapes.

In free-surface flow, the nature of the flow (supercritical or subcritical) depends upon whether the Froude number is greater than or less than unity.

See also