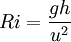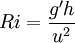Richardson number

The Richardson number is named after Lewis Fry Richardson (1881 - 1953). It is the dimensionless number that expresses the ratio of potential to kinetic energy ^[1]

Additional recommended knowledge

Guide to balance cleaning: 8 simple steps

Weighing the right way

Essential Laboratory Skills Guide

where g is the acceleration due to gravity, h a representative vertical lengthscale, and u a representative speed.

When considering flows in which density differences are small (the Boussinesq approximation), it is common to use the reduced gravity g' and the relevant parameter is the densimetric Richardson number

which is used frequently when considering atmospheric or oceanic flows.

If the Richardson number is much less than unity, buoyancy is unimportant in the flow. If it is much greater than unity, buoyancy is dominant (in the sense that there is insufficient kinetic energy to homogenize the fluids).

If the Richardson number is of order unity, then the flow is likely to be buoyancy-driven: the energy of the flow derives from the potential energy in the system originally.

Aviation

In aviation, the Richardson number is used as a rough measure of expected air turbulence. A lower score indicates a higher degree of turbulence. Values in the range 10 to 0.1 are typical, with values below unity indicating significant turbulence.

Oceanography

In oceanography, the Richardson number has a more general form which takes stratification into account. It is a measure of relative importance of mechanical and density effects in the water column.

Ri = N² / (du / dz)²

where N is the Brunt-Väisälä frequency.

The Richardson number defined above is always considered positive. An imaginary N indicates unstable density gradients with active convective overturning. Under such circumstances, N does not have an accepted quantitative meaning and the magnitude of negative Ri is not generally of interest. When Ri is small (typically considered below 1/4), then velocity shear is considered sufficient to overcome the tendency of a stratified fluid to remain stratified, and some mixing will generally occur. When Ri is large, turbulent mixing across the stratification is generally suppressed. A good reference on this subject is J.S. Turner, Buoyancy Effects in Fluids, Cambridge University Press, 1973.

Notes

1. ^ Modellers will be more familiar with the reciprocal of the square root of the Richardson number, known as the Froude number.