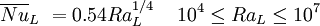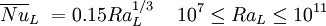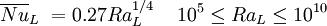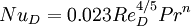Nusselt number

The Nusselt number is a dimensionless number which quantifies convective heat transfer from a surface. It is named after Wilhelm Nusselt.

where

• L = characteristic length
• k_f = thermal conductivity of the fluid
• h = convective heat transfer coefficient

Selection of the characteristic length should be in the direction of growth of the boundary layer. For complex shapes, the length scale may be defined as the volume of the body divided by the surface area. Several simple examples of characteristic length scale would be the diameter of a cylinder in cross flow, the length of a vertical plate undergoing natural convection, or the diameter of a sphere. Note that the fluid thermal conductivity is typically (but not always) evaluated at the film temperature which for engineering purposes may be calculated as the average of the bulk fluid temperature and surface temperature.

For relations defined as a local Nusselt number, one should use the distance at the point of interest as the characteristic length. To obtain an average Nusselt number however, one must integrate said relation over the entire characteristic length. Typically the average Nusselt number has the form Nu = f(Ra, Pr). Empirical correlations for a wide variety of gemoetries are available that express the Nusselt number in the aformentioned form.

The mass transfer analog of the Nusselt number is the Sherwood number.

Additional recommended knowledge

Guide to balance cleaning: 8 simple steps

How to quickly check pipettes?

Safe Weighing Range Ensures Accurate Results

Empirical calculations

Free convection at a vertical wall

Cited as coming from Churchill and Chu^[1]

Free convection from horizontal plates

For the top surface of a hot object in a colder environment or bottom surface of a cold object in a hotter environment^[1]

For the bottom surface of a hot object in a colder environment or top surface of a cold object in a hotter environment^[1]

Forced convection in pipe flow

The Dittus-Boelter equation (for turbulent flow), with n=0.4 for heating of the fluid, and n=0.3 for cooling of the fluid^[1]:

See also

• Churchill-Bernstein Equation

References

1. ^ ^{a b c d} Incropera, Frank P.; DeWitt, David P.. Fundamentals of Heat and Mass Transfer, 4th Edition, Wiley. p 493