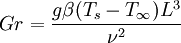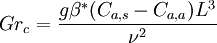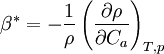My watch list
my.chemeurope.com  

my.chemeurope.com

With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.

  • My watch list
  • My saved searches
  • My saved topics
  • My newsletter
Register free of charge
Login  
eng  
DeutschEnglishFrançaisEspañol

Grashof number



The Grashof number is a dimensionless number in fluid dynamics which approximates the ratio of the buoyancy to viscous force acting on a fluid. It is named after the German engineer Franz Grashof.

Gr = \frac{g \beta (T_s - T_\infty ) L^3}{\nu ^2}\,

where

g = acceleration due to Earth's gravity
β = volumetric thermal expansion coefficient
Ts = source temperature
T∞ = quiescent temperature
L = characteristic length
ν = kinematic viscosity

The product of the Grashof number and the Prandtl number gives the Rayleigh number, a dimensionless number that characterizes convection problems in heat transfer.

There is an analogous form of the Grashof number used in cases of natural convection mass transfer problems.

Gr_c = \frac{g \beta^* (C_{a,s} - C_{a,a} ) L^3}{\nu^2}

where

\beta^* = -\frac{1}{\rho} \left ( \frac{\partial \rho}{\partial C_a} \right )_{T,p}

and

g = acceleration due to Earth's gravity
Ca,s = concentration of species a at surface
Ca,a = concentration of species a in ambient medium
L = characteristic length
ν = kinematic viscosity
ρ = fluid density
Ca = concentration of species a
T = constant temperature
p = constant pressure

See also

v • d • e
Dimensionless numbers in fluid dynamics
Archimedes • Bagnold • Biot • Bond • Brinkman • Capillary • Damköhler • Dean • Deborah • Eckert • Ekman • Eötvös • Euler • Froude • Galilei • Grashof • Hagen • Knudsen • Laplace • Lewis • Mach • Magnetic Reynolds • Marangoni • Morton • Nusselt • Ohnesorge • Péclet • Prandtl • Rayleigh • Reynolds • Richardson • Roshko • Rossby• Ruark • Schmidt • Sherwood • Stanton • Stokes • Strouhal • Suratman • Taylor • Weber • Weissenberg • Womersley

References

  • Jaluria, Yogesh. Natural Convection Heat and Mass Transfer (New York: Pergamon Press, 1980).
 
This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Grashof_number". A list of authors is available in Wikipedia.
Your browser is not current. Microsoft Internet Explorer 6.0 does not support some functions on Chemie.DE