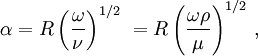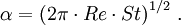Womersley number

A Womersley number is a dimensionless number in biofluid mechanics. It is a dimensionless expression of the of pulsatile flow frequency in relation to viscous effects. It is named after John R. Womersley (1907-1958).

Additional recommended knowledge

What is the Correct Way to Check Repeatability in Balances?

How to quickly check pipettes?

Daily Sensitivity Test

The Womersley number, usually denoted α, can be written as

where R is an appropriate length scale (for example the radius of a pipe), ω is the angular frequency of the oscillations, and ν, ρ, μ are the kinematic viscosity, density, and dynamic viscosity of the fluid, respectively. It can also be written in terms of the dimensionless Reynolds number (Re) and Strouhal number (St):

The Womersley number arises in the solution of the linearized Navier Stokes equations for oscillatory flow (presumed to be laminar and incompressible) in a tube. When α is small (1 or less), it means the frequency of pulsations is sufficiently low that a parabolic velocity profile has time to develop during each cycle, and the flow will be very nearly in phase with the pressure gradient, and will be given to a good approximation by Poiseuille's law, using the instantaneous pressure gradient. When α is large (10 or more), it means the frequency of pulsations is sufficiently large that the velocity profile is relatively flat or plug-like, and the mean flow lags the pressure gradient by about 90 degrees.

In a flow distribution network that progresses from a large tube to many small tubes (e.g. a blood vessel network), the frequency, density, and dynamic viscosity are (usually) the same throughout the network, but the tube radii change. Therefore the Womersley number is large in large vessels and small in small vessels.

It has been argued (West et al., 1997) that universal biological scaling laws (power-law relationships that describe variation of quantities such as metabolic rate, lifespan, length, etc., with body mass) are a consequence of the need for energy minimization, the fractal nature of vascular networks, and the crossover from high to low Womersley number flow as one progresses from large to small vessels.

References

• Nichols, W.W., O'Rourke, M.F. (2005). McDonald's Blood Flow in Arteries, London: Hodder-Arnold.
• West, G.B., Brown, J.H., Enquist, B.J. (1997). "A general model for the origin of allometric scaling laws in biology", Science 276: 122-126.
• [1] Womersley, J.R. (1955). "Method for the calculation of velocity, rate flow, and viscous drag in arteries when the pressure gradient is known," Journal of Physiology, Vol 127, pp. 553–563.