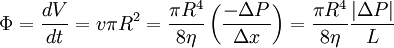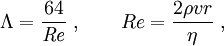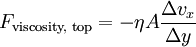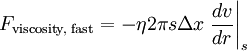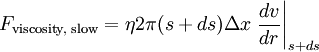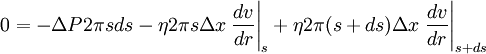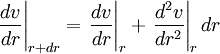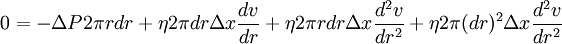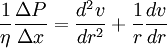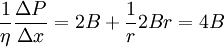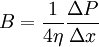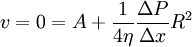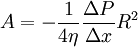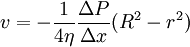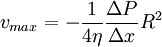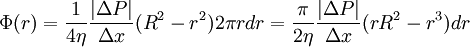To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Poiseuille's lawPoiseuille's law is the physical law concerning the voluminal laminar stationary flow Φ of an incompressible uniform viscous liquid (so called Newtonian fluid) through a cylindrical tube with constant circular cross-section. Poiseuille's law is also sometimes called the Hagen-Poiseuille law including reference to Gotthilf Heinrich Ludwig Hagen (1797-1884) for his experiments in 1839. Poiseuille's law was experimentally derived in 1838 and formulated and published in 1840 and 1846 by Jean Louis Marie Poiseuille (1797-1869). Poiseuille's law may be expressed in the following form: where V is a volume of the liquid, poured in the time unit t, v the mean fluid velocity along the length of the tube, x the direction of flow, R the internal radius of the tube, ΔP the pressure difference between the two ends, η the dynamic fluid viscosity, and L the total length of the tube in the x direction. This result is also a solution to the phenomenological Darcy-Weisbach equation in the field of hydraulics, given a relationship for the friction factor in terms of the Reynolds number: where Re is the Reynolds number and ρ fluid density. In this form the law approximates the Darcy friction factor, the energy (head) loss factor, friction loss factor or Darcy (friction) factor Λ in the laminar flow at very low velocities in cylindrical tube. The theoretical derivation of a slightly different form of the law was made independently by Wiedman in 1856 and Neumann and E. Hagenbach in 1858 (1859, 1860). Hagenbach was the first who called this law the Poiseuille's law. The law is also very important specially in hemorheology and hemodynamics, both fields of physiology.[1] The Poiseuilles' law was later in 1891 extended to turbulent flow by L. R. Wilberforce, based on Hagenbach's work. Product highlight
DerivationViscosityThe derivation of Poiseuille's Law is surprisingly simple, but it requires an understanding of Viscosity. When two layers of liquid in contact with each other move at different speeds, there will be a force between them. This force is proportional to the area of contact A, the velocity difference in the direction of flow Δvx/Δy, and a proportionality constant η and is given by The negative sign is in there because we are concerned with the faster moving liquid (top in figure), which is being slowed by the slower liquid (bottom in figure). By Newton's third law of motion, the force on the slower liquid is equal and opposite (no negative sign) to the force on the faster liquid. This equation assumes that the area of contact is so large that we can ignore any effects from the edges and that the fluids behave as Newtonian fluids. Liquid flow through a pipeIn a tube we make a basic assumption: the liquid in the center is moving fastest while the liquid touching the walls of the tube is stationary (due to friction). To simplify the situation, let's assume that there are a bunch of circular layers (lamina) of liquid, each having a velocity determined only by their radial distance from the center of the tube. To figure out the motion of the liquid, we need to know all forces acting on each lamina:
The first of these forces comes from the definition of pressure. The other two forces require us to modify the equations above that we have for viscosity. In fact, we are not modifying the equations, instead merely plugging in values specific to our problem. Let's focus on the pull from the faster lamina (#2) first. Faster laminaAssume that we are figuring out the force on the lamina with radius s. From the equation above, we need to know the area of contact and the velocity gradient. Think of the lamina as a cylinder of radius s and thickness ds. The area of contact between the lamina and the faster one is simply the area of the inside of the cylinder: A = 2πsΔx. We don't know the exact form for the velocity of the liquid within the tube yet, but we do know (from our assumption above) that it is dependent on the radius. Therefore, the velocity gradient is the change of the velocity with respect to the change in the radius at the intersection of these two laminae. That intersection is at a radius of s. So, considering that this force will be positive with respect to the movement of the liquid (but the derivative of the velocity is negative), the final form of the equation becomes where the vertical bar and subscript s following the derivative indicates that it should be taken at a radius of s. Slower laminaNext let's find the force of drag from the slower lamina. We need to calculate the same values that we did for the force from the faster lamina. In this case, the area of contact is at s+ds instead of s. Also, we need to remember that this force opposes the direction of movement of the liquid and will therefore be negative (and that the derivative of the velocity is negative). Putting it all togetherTo find the solution for the flow of liquid through a tube, we need to make one last assumption. There is no acceleration of liquid in the pipe, and by Newton's first law, there is no net force. If there is no net force then we can add all of the forces together to get zero
or Before we move further, we need to simplify this ugly equation. First, to get everything happening at the same point, we need to do a Taylor series expansion of the velocity gradient, keeping only the linear and quadratic terms (a standard mathematical trick). Let's use this relation in our equation. Also, let's use r instead of s since the lamina we chose was arbitrary and we want our expression to be valid for all laminae. Grouping like terms and dropping the vertical bar since all derivatives are assumed to be at radius r, Finally, let's get this in the form of a differential equation, moving some terms around to make it easier to solve later, and neglecting the term quadratic in dr since this will be really small compared to the rest (another standard mathematical trick). It can be seen that both sides of the equations are negative: there is a drop of pressure along the tube (left side) and both first and second derivatives of the velocity are negative (velocity has a maximum value of the center of the tube). This type of differential equation has solutions of the form v = A+Br2. To solve, we will substitute this into our equation and solve for A and B. this means that to solve for A we'll use the assumption we made at the beginning that at the wall of the tube (r = R) the velocity must be 0. or Now we have a formula for the velocity of liquid moving through the tube as a function of the distance from the center of the tube or, at the center of the tube where the liquid is moving fastest (r = 0) with R being the radius of the tube, Poiseuille's LawTo get the total volume that flows through the tube, we need to add up the contributions from each lamina. To calculate the flow through each lamina, we multiply the velocity (from above) and the area of the lamina. Finally, we integrate over all lamina via the radius variable r. Electrical Circuits analogyElectricity was originally understood to be a kind of fluid. This hydraulic analogy is still conceptually useful. Poiseuille's law corresponds to Ohm's law for electrical circuits (V = IR), where the pressure drop ΔP is analogous to the voltage V and voluminal flow rate Φ is analogous to the current I. Then the resistance This concept is useful because the effective resistance in a tube is inversely proportional to the fourth power of the radius. This means that halfing the size of the tube increases the resistance to fluid movement by 16 times. Both Ohm's law and Poiseuille's law illustrate transport phenomena. References
See also
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Poiseuille's_law". A list of authors is available in Wikipedia. |
- Oleochemicals to Benefit from Demand for Sustainable Chemicals - Bio-compatible equivalents of petrochemicals, they help reduce carbon footprint and are safer
- SHIFTGURU | Libro di turno digitale | iMes Solutions
- Enhanced Supply Critical as Refined Glycerine Gains Prominence Across New Application Sectors