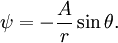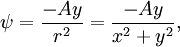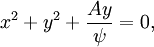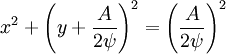To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Potential flowA potential flow is characterized by an irrotational velocity field. This property allows the description of the velocity field as the gradient of a scalar function (because taking the curl of the gradient is equivalent to make the cross product of two parallel vectors which is always zero). The flow can be compressible or incompressible, stationary or unstationary. The free-vortex flow is a solution of the vorticity transport equation (obtained by taking the curl of the Euler momentum equation) only if the sources terms are zero, that is that the flow is barotropic (the pressure varies only with the density) and that the external forces are negligible or derives from a potential (the force fields are described by taking the gradient of scalar functions). In incompressible, steady or unsteady, fluid dynamics, potential flow obeys the following equations
Note that " The equations above imply Together with the Navier-Stokes equations or the Euler equations, these equations can be used to calculate solutions to many practical flow situations. In two dimensions, potential flow reduces to a very simple system that is analyzed using complex numbers (see below). Potential flow does not include all the characteristics of flows that are encountered in the real world. For example, potential flow excludes turbulence, which is commonly encountered in nature. Richard Feynman considered potential flow to be so unphysical that the only fluid to obey the assumptions was "dry water". Potential flow also makes a number of invalid predictions, such as d'Alembert's paradox, which states that the drag on any object moving through an infinite fluid otherwise at rest is zero. More precisely, potential flow cannot account for the behaviour of flows that include a boundary layer. Nevertheless, understanding potential flow is important in many branches of fluid mechanics. In particular, simple potential flows (called elemental flows) such as the free vortex and the point source possess ready analytical solutions. These solutions can be superposed to create more complex flows satisfying a variety of boundary conditions. These flows correspond closely to real-life flows over the whole of fluid mechanics; in addition, many valuable insights arise when considering the deviation (often slight) between an observed flow and the corresponding potential flow. Potential flow finds many applications in fields such as aircraft design. For instance, in computational fluid dynamics, one technique is to couple a potential flow solution outside the boundary layer to a solution of the boundary layer equations inside the boundary layer. The absence of boundary layer effects means that any streamline can be replaced by a solid boundary with no change in the flow field, a technique used in many aerodynamic design approaches. Another technique would be the use of Riabouchinsky solids. Product highlight
AnalysisPotential flow in two dimensions is simple to analyze using complex numbers, viewed for convenience on the Argand diagram. The basic idea is to define a holomorphic function f. If we write
then the Cauchy-Riemann equations show that (it is conventional to regard all symbols as real numbers; and to write z = x + iy and w = φ + iψ). Also notice that The velocity field then satisfies the requirements for potential flow: and ψ is defined as the stream function. Lines of constant ψ are known as streamlines and lines of constant φ are known as equipotential lines (see equipotential surface). The two sets of curves intersect at right angles, for Examples: general considerationsAny differentiable function may be used for f. The examples that follow use a variety of elementary functions; special functions may also be used. Note that multi-valued functions such as the natural logarithm may be used, but attention must be confined to a single Riemann surface. Examples: Power lawsIf
then, writing x + iy = reiθ, we have
and
Power law with n = 1If w = Az1, that is, a power law with n = 1, the streamlines (ie lines of constant ψ) are a system of straight lines parallel to the x-axis. This is easiest to see by writing in terms of real and imaginary components: thus giving φ = Ax and ψ = Ay. Power law with n = 2If n = 2, then w = Az2 and the streamline corresponding to a particular value of ψ are those points satisfying
which is a system of rectangular hyperbolae. This may be seen by again rewriting in terms of real and imaginary components. Noting that
The velocity field is given by In fluid dynamics, the flowfield near the origin corresponds to a stagnation point. Note that the fluid at the origin is at rest (this follows on differentiation of f(z) = z2 at z = 0). The ψ = 0 streamline is particularly interesting: it has two (or four) branches, following the coordinate axes, ie x = 0 and y = 0. As no fluid flows across the x-axis, it (the x-axis) may be treated as a solid boundary. It is thus possible to ignore the flow in the lower half-plane where y < 0 and to focus on the flow in the upper half-plane. With this interpretation, the flow is that of a vertically directed jet impinging on a horizontal flat plate. The flow may also be interpreted as flow into a 90 degree corner if the regions specified by (say) x < 0 and y < 0 are ignored. Power law with n = 3If n = 3 the resulting flow is a sort of hexagonal version of the n = 2 case considered above. Streamlines are given by 3x2y − y3 = ψ. Power law with n = − 1if This is more easily interpreted in terms of real and imaginary components: Thus the streamlines are circles that are tangent to the x-axis at the origin. The velocity field is given by The circles in the upper half-plane thus flow clockwise, those in the lower half-plane flow anticlockwise. Note that speeds go as r − 2; and the speed at the origin is infinite. Power law with n = − 2{this section is to be completed} See also
|
|||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Potential_flow". A list of authors is available in Wikipedia. |


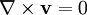 (zero rotation)
(zero rotation)
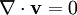 (zero divergence = volume conservation)
(zero divergence = volume conservation)
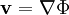
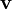 is the fluid velocity vector
is the fluid velocity vector
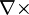 " is curl
" is curl
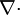 " is divergence.
" is divergence.
 " is gradient
" is gradient
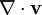 " is not formally equivalent to "
" is not formally equivalent to "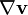 ": the former quantity is a scalar, while the latter is a tensor.
": the former quantity is a scalar, while the latter is a tensor.
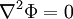 , or Laplace's equation, holds.
, or Laplace's equation, holds.



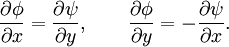
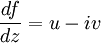 (Some steps are missing, try calculating yourself)
(Some steps are missing, try calculating yourself)
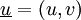 , specified by
, specified by
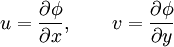
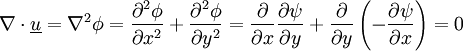
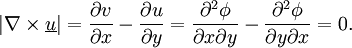
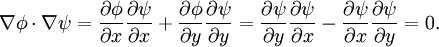
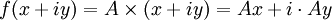
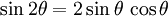 and rewriting
and rewriting 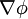 , or
, or
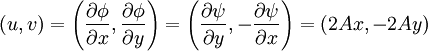
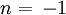 , the streamlines are given by
, the streamlines are given by