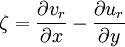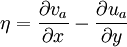To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
VorticityVorticity is a mathematical concept used in fluid dynamics. It can be related to the amount of "circulation" or "rotation" (or more strictly, the local angular rate of rotation) in a fluid. The average vorticity in a small region of fluid flow is equal to the circulation Γ around the boundary of the small region, divided by the area A of the small region.
Product highlight
Fluid dynamicsIn fluid dynamics, vorticity is the curl of the fluid velocity. It can also be considered as the circulation per unit area at a point in a fluid flow field. It is a vector quantity, whose direction is along the axis of the fluid's rotation. For a two-dimensional flow, the vorticity vector is perpendicular to the plane. For a fluid having locally a "rigid rotation" around an axis (i.e., moving like a rotating cylinder), vorticity is twice the angular velocity of a fluid element. An irrotational fluid is one whose vorticity=0. Somewhat counter-intuitively, an irrotational fluid can have a non-zero angular velocity (e.g. a fluid rotating around an axis with its tangential velocity inversely proportional to the distance to the axis has a zero vorticity) (see also forced and free vortex) One way to visualize vorticity is this: consider a fluid flowing. Imagine that some tiny part of the fluid is instantaneously rendered solid, and the rest of the flow removed. If that tiny new solid particle would be rotating, rather than just translating, then there is vorticity in the flow.
In general, vorticity is a specially powerful concept in the case that the viscosity is low (i.e. high Reynolds number). In such cases, even when the velocity field is relatively complicated, the vorticity field can be well approximated as zero nearly everywhere except in a small region in space. This is clearly true in the case of 2-D potential flow (i.e. 2-D zero viscosity flow), in which case the flowfield can be identified with the complex plane, and questions about those sorts of flows can be posed as questions in complex analysis which can often be solved (or approximated very well) analytically. For any flow, you can write the equations of the flow in terms of vorticity rather than velocity by simply taking the curl of the flow equations that are framed in terms of velocity (may have to apply the 2nd Fundamental Theorem of Calculus to do this rigorously). In such a case you get the vorticity transport equation which is as follows in the case of incompressible (i.e. low mach number) fluids, with conservative body forces: Even for real flows (3-dimensional and finite Re), the idea of viewing things in terms of vorticity is still very powerful. It provides the most useful way to understand how the potential flow solutions can be perturbed for "real flows." In particular, one restricts attention to the vortex dynamics, which presumes that the vorticity field can be modeled well in terms of discrete vortices (which encompasses a large number of interesting and relevant flows). In general, the presence of viscosity causes a diffusion of vorticity away from these small regions (e.g. discrete vortices) into the general flow field. This can be seen by the diffusion term in the vorticity transport equation. Thus, in cases of very viscous flows (e.g. Couette Flow), the vorticity will be diffused throughout the flow field and it is probably simpler to look at the velocity field (i.e. vectors of fluid motion) rather than look at the vorticity field (i.e. vectors of curl of fluid motion) which is less intuitive. Related concepts are the vortex-line, which is a line which is everywhere tangent to the local vorticity; and a vortex tube which is the surface in the fluid formed by all vortex-lines passing through a given (reducible) closed curve in the fluid. The 'strength' of a vortex-tube is the integral of the vorticity across a cross-section of the tube, and is the same at everywhere along the tube (because vorticity has zero divergence). It is a consequence of Helmholtz's theorems (or equivalently, of Kelvin's circulation theorem) that in an inviscid fluid the 'strength' of the vortex tube is also constant with time. Note however that in a three dimensional flow, vorticity (as measured by the volume integral of its square) can be intensified when a vortex-line is extended (see say Batchelor, section 5.2). Mechanisms such as these operate in such well known examples as the formation of a bath-tub vortex in out-flowing water, and the build-up of a tornado by rising air-currents. Vorticity Equation
The vorticity equation describes the evolution of the vorticity of a fluid element as it moves around. In fluid mechanics this equation can be expressed in vector form as follows, where, Atmospheric sciencesIn the atmospheric sciences, vorticity is the rotation of air around a vertical axis. Vorticity is a vector quantity and the direction of the vector is given by the right-hand rule with the fingers of the right hand indicating the direction and curvature of the wind. When the vorticity vector points upward into the atmosphere, vorticity is positive; when it points downward into the earth it is negative. Vorticity in the atmosphere is therefore positive for counter-clockwise rotation (looking down onto the earth's surface), and negative for clockwise rotation. In the Northern Hemisphere cyclonic rotation of the atmosphere is counter-clockwise so is associated with positive vorticity, and anti-cyclonic rotation is clockwise so is associated with negative vorticity. In the Southern Hemisphere cyclonic rotation is clockwise with negative vorticity; anti-cyclonic rotation is counter-clockwise with positive vorticity. Relative and absolute vorticity are defined as the z-components of the curls of relative (i.e., in relation to Earth's surface) and absolute wind velocity, respectively. This gives for relative vorticity and for absolute vorticity, where u and v are the zonal (x direction) and meridional (y direction) components of wind velocity. The absolute vorticity at a point can also be expressed as the sum of the relative vorticity at that point and the Coriolis parameter at that latitude (i.e., it is the sum of the Earth's vorticity and the vorticity of the air relative to the Earth). A useful related quantity is potential vorticity. The absolute vorticity of an air mass will change if the air mass is stretched (or compressed) in the z direction. But if the absolute vorticity is divided by the vertical spacing between levels of constant entropy (or potential temperature), the result is a conserved quantity of adiabatic flow, termed potential vorticity (PV). Because diabatic processes, which can change PV and entropy, occur relatively slowly in the atmosphere, PV is useful as an approximate tracer of air masses over the timescale of a few days, particularly when viewed on levels of constant entropy. The barotropic vorticity equation is the simplest way for forecasting the movement of Rossby waves (that is, the troughs and ridges of 500 hPa geopotential height) over a limited amount of time (a few days). In the 1950s, the first successful programs for numerical weather forecasting utilized that equation. In modern numerical weather forecasting models and GCMs, vorticity may be one of the predicted variables, in which case the corresponding time-dependent equation is a prognostic equation.
Other fieldsVorticity is important in many other areas of fluid dynamics. For instance, the lift distribution over a finite wing may be approximated by assuming that each segment of the wing has a semi-infinite trailing vortex behind it. It is then possible to solve for the strength of the vortices using the criterion that there be no flow induced through the surface of the wing. This procedure is called the vortex panel method of computational fluid dynamics. The strengths of the vortices are then summed to find the total approximate circulation about the wing. According to the Kutta-Joukowski theorem, lift is the product of circulation, airspeed, and air density. See also
Atmospheric sciences
Fluid dynamics
Further reading
References
|
|||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Vorticity". A list of authors is available in Wikipedia. |


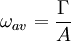
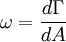




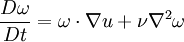
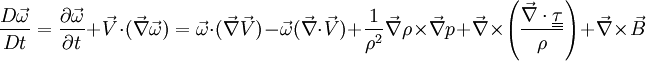
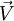 is the velocity vector,
is the velocity vector, 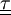 is the viscous stress tensor and
is the viscous stress tensor and 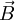 is the body force term. The equation is valid for compressible fluid in the absence of any concentrated torques and line forces. No assumption is made regarding the relationship between the stress and the rate of strain tensors (c.f.
is the body force term. The equation is valid for compressible fluid in the absence of any concentrated torques and line forces. No assumption is made regarding the relationship between the stress and the rate of strain tensors (c.f.