Helmholtz's theorems

In fluid mechanics, Helmholtz's theorems (pub. 1858) describe the motion of vortex lines and tubes in a fluid. These theorems apply to inviscid barotropic fluid under the influence of a conservative body force^[1]

Product highlight

Identify raw materials immediately - without waiting time

Revolutionize your production: real-time Raman analysis for maximum efficiency

Efficient inline analysis for liquids and solids

The three theorems state:

1. Fluid elements initially free of vorticity remain free of vorticity.
2. Fluid elements lying on a vortex line at some instant continue to lie on that vortex line. More simply, vortex lines move with the fluid.
3. The strength of a vortex tube does not vary with time.^[2]

A corollary to the first law states that in an inviscid barotropic fluid, with conservative body forces, vortex lines and tubes must appear as a closed loop or extend to infinity or start/end at solid boundaries.

The theorems are now generally proven with reference to Kelvin's circulation theorem, however the Helmholtz's theorems were published nine years before the 1867 publication of Kelvin's theorem. There was much communication between the two men on the subject of vortex lines, with many references to the application of their theorems to the study of smoke rings.

Notes

1. ^ A body force is one which is proportional to mass/volume/charge on a body. Such forces act over the whole volume of the body as opposed to a surface forces which act only on the surface. Examples of body forces are gravitational force, electromagnetic force, etc. Examples of surface forces are friction, pressure force, etc. Also there are line forces, like surface tension.
2. ^ The strength of a vortex tube (circulation), is defined as:

   

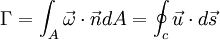
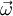   where Γ is also the circulation, is the vorticity vector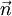, is the normal vector to a surface A, formed by taking a cross-section of the vortex-tube with elemental area dA, 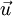is the velocity vector on the closed curve C, which bounds the surface A. The convention for defining the sense of circulation and the normal to the surface A is given by the right-hand screw rule. The third theorem states that this strength is the same for all cross-sections A of the tube and is independent of time. This is equivalent to saying

   .

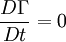See also

Kelvin's circulation theorem

References

• M. J. Lighthill, An Informal Introduction to Theoretical Fluid Mechanics, Oxford University Press, 1986, ISBN 0-19-853630-5
• P. G. Saffman, Vortex Dynamics, Cambridge University Press, 1995, ISBN 0-521-42058-X
• G. K. Batchelor, An Introduction to Fluid Dynamics, Cambridge University Press (1967, reprinted in 2000).
• Kundu, P and Cohen, I, "Fluid Mechanics", 2nd edition, Academic Press 2002.