To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Kelvin's circulation theoremIn fluid mechanics, Kelvin's Circulation Theorem states "In an inviscid, barotropic flow with conservative body forces, the circulation around a closed curve moving with the fluid remains constant with time"[1]. The theorem was developed by William Thomson, 1st Baron Kelvin. Stated mathematically: Product highlightwhere Γ is the circulation around a material contour C(t). Stated more simply this theorem says that if one observes a closed contour at one instant, and follows the contour over time (by following the motion of all of its fluid elements), the circulation over the two locations of this contour are equal. This theorem does not hold in cases with viscous stresses, nonconservative body forces (for example a coriolis force) or non-barotropic pressure-density relations. Mathematical ProofThe circulation Γ around a closed material contour C(t) is defined by: where u is the velocity vector, and ds is an element along the closed contour. The governing equation for an inviscid fluid with a conservative body force is where D/Dt is the convective derivative, ρ is the fluid density, p is the pressure and Φ is the potential for the body force. These are the Euler equations with a body force. The condition of baratropicity implies that the density is a function only of the pressure, i.e. ρ = ρ(p).
For the first term, we substitute from the governing equation, and then apply Stoke's theorem, thus: The final equality arises since For the second term, we note that evolution of the material line element is given by Hence The last equality is obtained by applying Stokes theorem. Since both terms are zero, we obtain the result See alsoReferences
Categories: Equations of fluid dynamics | Fluid dynamics |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Kelvin's_circulation_theorem". A list of authors is available in Wikipedia. |


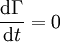



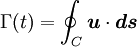
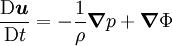
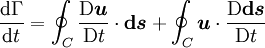
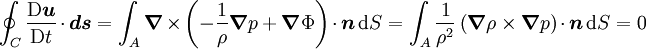
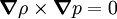 owing to baratropicity.
owing to baratropicity.
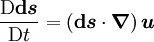
![\oint_C \boldsymbol{u} \cdot \frac{\mathrm{D} \boldsymbol{\mathrm{d}s}}{\mathrm{D}t} = \oint_C \boldsymbol{u} \cdot \left[ \left( \boldsymbol{\mathrm{d}s} \cdot \boldsymbol{\nabla} \right) \boldsymbol{u} \right] = \frac{1}{2} \oint_C \boldsymbol{\nabla} \left( |\boldsymbol{u}|^2 \right) \cdot \boldsymbol{\mathrm{d}s} = 0](images/math/4/8/4/4847b76996bf6da0d325bcb815d989ee.png)


