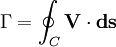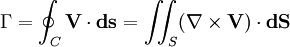To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Circulation (fluid dynamics)In fluid dynamics, circulation is the line integral around a closed curve of the fluid velocity. Circulation is normally denoted Γ. If Product highlightThe dimensions of circulation are length squared over time. Circulation was first used independently by Frederick Lanchester, Wilhelm Kutta, and Nikolai Zhukovsky. Kutta-Joukowski TheoremThe lift force acting per unit span on a body in an inviscid flow field can be expressed as the product of the circulation (Γ) about the body, the fluid density (ρ ), and the speed of the body relative to the free-stream (V). Thus,
This is known as the Kutta-Joukowski theorem. This equation applies both around airfoils, where the circulation is generated by airfoil action, and around spinning objects, experiencing the Magnus effect, where the circulation is induced mechanically. Circulation is often used in computational fluid dynamics as an intermediate variable to calculate forces on an airfoil or other body. The circulation around an airfoil can be finite, but the vorticity of the fluid outside of the airfoil can be zero. Relation to vorticityCirculation can be related to vorticity by Stokes' theorem: but only if the integration path is a boundary, not just a closed cycle. Thus vorticity is the circulation per unit area, taken around an infinitesimal loop. See also
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Circulation_(fluid_dynamics)". A list of authors is available in Wikipedia. |


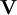 is the fluid velocity and
is the fluid velocity and 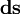 is a unit vector along the closed curve
is a unit vector along the closed curve