To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Barotropic vorticity equationA simplified form of the vorticity equation for an inviscid, divergence-free flow, the barotropic vorticity equation can simply be stated as Product highlightwhere
is absolute vorticity, with ζ being relative vorticity, defined as the vertical component of the curl of the fluid velocity and f is the Coriolis parameter
where Ω is the angular frequency of the planet's rotation (Ω=0.7272*10-4 s-1 for the earth) and φ is latitude. In terms of relative vorticity, the equation can be rewritten as where In 1950, Charney, Fjorloft, and von Neumann integrated this equation (with an added diffusion term on the RHS) on a computer for the first time, using an observed field of 500 hPa geopotential height for the first timestep. This was the one of the first successful instances of numerical weather forecasting. |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Barotropic_vorticity_equation". A list of authors is available in Wikipedia. |


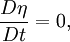



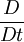 is the
is the 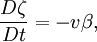
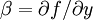 is the variation of the Coriolis parameter with distance
is the variation of the Coriolis parameter with distance 

