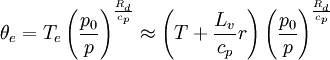Equivalent potential temperature

Equivalent potential temperature, commonly referred to as Theta-e , is a quantity related to the stability of a column of air in the atmosphere.

θ_e is the temperature a parcel of air would reach if all the water vapor in the parcel were to condense, releasing its latent heat, and the parcel was brought adiabatically to a pressure of 100 kPa (1000 mbar), roughly equal to atmospheric pressure at sea level. In stable conditions, θ_e increases with altitude. If θ_e decreases with height, convection can occur. The comparison of the equivalent potential temperature of parcels of air at different pressures thus provides a measure of the instability of the column of air.^[1]

Additional recommended knowledge

Guide to balance cleaning: 8 simple steps

Don't let static charges disrupt your weighing accuracy

How to quickly check pipettes?

Explanation

Stability

Cool air is denser (heavier) than warm air (see Gas laws). Like a ball balanced on top of a hill, denser fluid lying above less dense fluid is dynamically unstable: if cool air is positioned above warm air, the former will sink and the latter will rise, the two volumes of air passing around and through each other, and perhaps mixing to some extent, until a stable condition (with denser fluid below and lighter fluid above) is achieved. The temperature near the ceiling of a room is consistently warmer than that near the floor.

If a hydrostatic fluid is compressible, the criterion for dynamic stability is not simply that denser fluid must lie below light fluid, but that small perturbations must tend to correct themselves. When lower fluid is raised up into upper fluid, (during which process the density of the lower fluid decreases due to the drop in pressure), stability requires that it remain denser than the upper fluid, so that gravity pulls it back toward its original position. The fluid is unstable if small perturbations tend to amplify themselves, i.e. if dense lower fluid, when displaced upward, expands enough to become lighter than the surrounding upper fluid, and therefore continues to move upward.

Potential temperature

In the atmosphere, where vertical variation in pressure is much larger than in a room, the situation is complicated by adiabatic temperature change: as a parcel of air moves upward, the ambient pressure drops, causing the parcel to expand. Some of the internal energy of the parcel is used up in doing the work required to expand against the atmospheric pressure, so the temperature of the parcel drops, even though it has not lost any heat. Conversely, a sinking parcel is compressed and becomes warmer even though no heat is added.

Air at the top of a mountain is usually colder than the air in the valley below, but the arrangement is not unstable: if a parcel of air from the valley were somehow lifted up to the top of the mountain, when it arrived it would be even colder than the air already there, due to adiabatic cooling; it would be heavier than the ambient air, and would sink back toward its original position. Similarly, if a parcel of cold mountain-top air were to make the trip down to the valley, it would arrive warmer and lighter than the valley air, and would float back up the mountain.

So cool air lying on top of warm air can be stable after all (as long as the temperature decrease with height is less than the adiabatic lapse rate); the dynamically important quantity is not the temperature, but the potential temperature—the temperature the air would have if it were brought adiabatically to a reference pressure. The air around the mountain is stable because the air at the top, due to its lower pressure, has a higher potential temperature than the warmer air below.

Water vapor

A parcel of air containing water vapor, if it rises far enough, cools to its dew point: it becomes saturated with water vapor. This occurs because the vapor pressure of water decreases at lower temperatures (see Clausius-Clapeyron relation). If the parcel of air continues to rise, water vapor begins to condense into liquid droplets. The condensing water releases its latent heat to the surrounding air, partially offsetting the adiabatic cooling. A saturated parcel of air therefore cools less than a dry one would as it rises (its temperature changes with height at the moist adiabatic lapse rate, which is smaller than the dry adiabatic lapse rate).

Saturated air can be unstable even though its potential temperature increases with height: if the warming due to condensation is enough that a parcel of saturated air which is displaced upward (and would otherwise cool to below the ambient temperature) ends up warmer (lighter) than the surrounding air, it will continue to rise. This is the reason for defining the equivalent potential temperature, in analogy with the potential temperature: potential temperature is a temperature adjusted for potential warming due to adiabatic compression; equivalent potential temperature factors in potential warming due to condensation as well. For saturated air, or for air which is likely to be lifted high enough to reach saturation, it is the equivalent potential temperature which must increase with height in order to ensure stability.

Formula

The formula for θ_e is the following:^[2]

Where:

• T_e = equivalent temperature
• T = Temperature of air at pressure p
• p = pressure at the point (in same units as p₀)
• p₀ = standard reference pressure (1000 mbar or 100 kPa)
• R_d = specific gas constant for air (287 J/(kg·K))
• c_p = specific heat of dry air at constant pressure (1004 J/(kg·K))
• L_v = latent heat of evaporation (2400 kJ/kg {at 25 °C} to 2600 kJ/kg {at −40 °C})
• r = mixing ratio of water vapor in air

See also

• meteorology
• weather forecasting
• potential temperature

Bibliography

• M K Yau and R.R. Rogers, Short Course in Cloud Physics, Third Edition, published by Butterworth-Heinemann, January 1, 1989, 304 pages. EAN 9780750632157 ISBN 0-7506-3215-1

References