To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Clausius-Clapeyron relationThe Clausius-Clapeyron relation, named after Rudolf Clausius and Émile Clapeyron, is a way of characterizing the phase transition between two states of matter, such as solid and liquid. On a pressure-temperature (P-T) diagram, the line separating the two phases is known as the coexistence curve. The Clausius-Clapeyron relation gives the slope of this curve. Mathematically, where dP / dT is the slope of the coexistence curve, L is the latent heat, T is the temperature, and ΔV is the volume change of the phase transition. Product highlight
DisambiguationThe generalized equation given in the opening of this article is sometimes called the Clapeyron equation, while a less general form is sometimes called the Clausius-Clapeyron equation. The less general form neglects the magnitude of the specific volume of the liquid (or solid) state relative to that of the gas state and also approximates the specific volume of the gas state via the ideal gas law.[1] DerivationUsing the state postulate, take the specific entropy, s, for a homogeneous substance to be a function of specific volume, v, and temperature, T.[1] During a phase change, the temperature is constant, so[1]
Using the appropriate Maxwell relation gives[1]
Since temperature and pressure are constant during a phase change, the derivative of pressure with respect to temperature is not a function of the specific volume.[2][3] Thus the partial derivative may be changed into a total derivative and be factored out when taking an integral from one phase to another,[1]
For a closed system undergoing an internally reversible process, the first law is
Using the definition of specific enthalpy, h, and the fact that the temperature and pressure are constant, we have[1]
After substitution of this result into the derivative of the pressure, one finds[4][1]
where the shift to capital letters indicates a shift to extensive variables. This last equation is called the Clausius-Clapeyron equation, though some thermodynamics texts just call it the Clapeyron equation, possibly to distinguish it from the approximation below. When the transition is to a gas phase, the final specific volume can be many times the size of the initial specific volume. A natural approximation would be to replace Δv with v2. Furthermore, at low pressures, the gas phase may be approximated by the ideal gas law, so that v2 = vgas = RT / P, where R is the mass specific gas constant (forcing h and v to be mass specific). Thus,[1]
This leads to a version of the Clausius-Clapeyron equation that is simpler to integrate:[1]
These last equations are useful because they relate saturation pressure and saturation temperature to the enthalpy of phase change, without requiring specific volume data. Other derivationSuppose two phases, I and II, are in contact and at equilibrium with each other. Then the chemical potentials are related by μI = μII. Along the coexistence curve, we also have dμI = dμII. We now use the Gibbs-Duhem relation dμ = − sdT + vdP, where s and v are, respectively, the entropy and volume per particle, to obtain Hence, rearranging, we have From the relation between heat and change of entropy in a reversible process δQ = T dS, we have that the quantity of heat added in the transformation is Combining the last two equations we obtain the standard relation. ApplicationsChemistry and chemical engineeringThe Clausius-Clapeyron equation for the liquid-vapor boundary may be used in either of two equivalent forms. where
This can be used to predict the temperature at a certain pressure, given the temperature at another pressure, or vice versa. Alternatively, if the corresponding temperature and pressure is known at two points, the enthalpy of vaporization can be determined. The equivalent formulation, in which the values associated with one P,T point are combined into a constant (the constant of integration as above), is For instance, if the p,T values are known for a series of data points along the phase boundary, then the enthalpy of vaporization may be determined from a plot of lnP against 1 / T. Notes:
Meteorology
In meteorology, a specific derivation of the Clausius-Clapeyron equation is used to describe dependence of saturated water vapor pressure on temperature. This is similar to its use in chemistry and chemical engineering. It plays a crucial role in the current debate on climate change because its solution predicts exponential behavior of saturation water vapor pressure (and, therefore water vapor concentration) as a function of temperature. In turn, because water vapor is a greenhouse gas, it might lead to further increase in the sea surface temperature leading to runaway greenhouse effect. Debate on iris hypothesis and intensity of tropical cyclones dependence on temperature depends in part on “Clausius-Clapeyron” solution. Clausius-Clapeyron equations is given for typical atmospheric conditions as where:
One can solve this equation to give[5] where:
Thus, neglecting the weak variation of (T+243.5) at normal temperatures, one observes that saturation water vapor pressure changes exponentially with T. ExampleOne of the uses of this equation is to determine if a phase transition will occur in a given situation. Consider the question of how much pressure is needed to melt ice at a temperature ΔT below 0 °C. We can assume and substituting in
we obtain
To provide a rough example of how much pressure this is, to melt ice at -7 °C (the temperature many ice skating rinks are set at) would require balancing a small car (mass = 1000 kg[6]) on a thimble (area = 1 cm²). References
Bibliography
Categories: Thermodynamics | Atmospheric thermodynamics | Chemical engineering |
|||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Clausius-Clapeyron_relation". A list of authors is available in Wikipedia. |


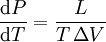



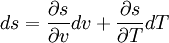
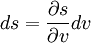 .
.
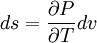 .
.
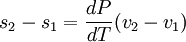 ,
,
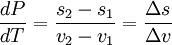 .
.
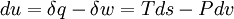 .
.
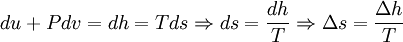 .
.
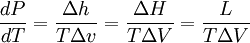 ,
,
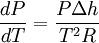 .
.
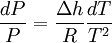 ,
,
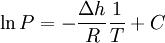 , or
, or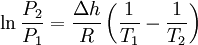 .
.
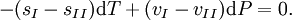
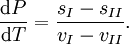
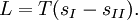
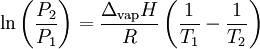
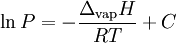
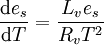
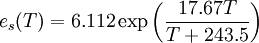
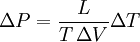
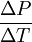 = -13.1 MPa/°C.
= -13.1 MPa/°C.


