To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Diabatic
In quantum chemistry, the potential energy surfaces are obtained within the adiabatic or Born-Oppenheimer approximation. This corresponds to a representation of the molecular wave function where the variables corresponding to the molecular geometry and the electronic degrees of freedom are separated. The non separable terms are due to the nuclear kinetic energy terms in the molecular Hamiltonian and are said to couple the potential energy surfaces. In the neighbourhood of an avoided crossing or conical intersection, these terms cannot be neglected. One therefore usually performs one unitary transformation from the adiabatic representation to the so-called diabatic representation in which the nuclear kinetic energy operator is diagonal. In this representation, the coupling is due to the electronic energy and is a scalar quantity which is much more easy to estimate numerically. Product highlightIn the diabatic representation, the potential energy surfaces are smoother so that low order Taylor series expansions of the surface capture much of the complexity of the original system. Unfortunately, strictly diabatic states do not exist in the general case. Hence, diabatic potentials generated from transforming multiple electronic energy surfaces together are generally not exact. These can be called pseudo-diabatic potentials, but generally the term is not used unless it is necessary to highlight this subtletly. Hence, pseudo-diabatic potentials are synonymous with diabatic potentials. ApplicabilityThe motivation to calculate diabatic potentials often occurs when the Born-Oppenheimer approximation does not hold, or is not justified for the molecular system under study. For these systems, it is necessary to go beyond the Born-Oppenheimer approximation. This is often the terminology used to refer to the study of nonadiabatic systems. A well-known approach involves recasting the molecular Schrödinger equation into a set of coupled eigenvalue equations. This is achieved by expansion of the exact wave function in terms of products of electronic and nuclear wave functions (adiabatic states) followed by integration over the electronic coordinates. The coupled operator equations thus obtained depend on nuclear coordinates only. Off-diagonal elements in these equations are nuclear kinetic energy terms. A diabatic transformation of the adiabatic states replaces these off-diagonal kinetic energy terms by potential energy terms. Sometimes, this is called the "adiabatic to diabatic transformation", abbreviated ADT.
Diabatic transformation of two electronic surfacesIn order to introduce the diabatic transformation we assume now, for the sake of argument, that only two Potential Energy Surfaces (PES), 1 and 2, approach each other and that all other surfaces are well separated; the argument can be generalized to more surfaces. Let the collection of electronic coordinates be indicated by The nuclear kinetic energy is a sum over nuclei A with mass MA, (Atomic units are used here). By applying the Leibniz rule for differentation, the matrix elements of Tn are (where we suppress coordinates for clarity reasons): The subscript the coupled Schrödinger equations for the nuclear part take the form (see the article Born-Oppenheimer approximation) In order to remove the problematic off-diagonal kinetic energy terms, we
define two new orthonormal states by a diabatic transformation of the adiabatic states where These elements are zero because Assume that a diabatic angle i.e., By a small change of notation these differential equations for It is well-known that the differential equations have a solution (i.e., the "potential" V exists) if and only if the vector field ("force")
It can be shown that these conditions are rarely ever satisfied, so that a strictly diabatic
transformation rarely ever exists. It is common to use approximate functions Under the assumption that the momentum operators are represented exactly by 2 x 2 matrices, which is consistent with neglect of off-diagonal elements other than the (1,2) element and the assumption of "strict" diabaticity, it can be shown that On the basis of the diabatic states the nuclear motion problem takes the following generalized Born-Oppenheimer form It is important to note that the off-diagonal elements depend on the diabatic angle and electronic energies only. The surfaces
References |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Diabatic". A list of authors is available in Wikipedia. |





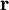 , while
, while 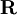 indicates dependence on nuclear coordinates. Thus, we assume
indicates dependence on nuclear coordinates. Thus, we assume 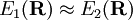 with corresponding orthonormal electronic eigenstates
with corresponding orthonormal electronic eigenstates
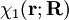 and
and 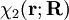 .
In the absence of magnetic interactions these electronic states, which depend parametrically on the nuclear coordinates, may be taken to be real-valued functions.
.
In the absence of magnetic interactions these electronic states, which depend parametrically on the nuclear coordinates, may be taken to be real-valued functions.
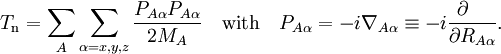
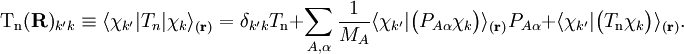
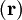 indicates that the integration inside the braket is
over electronic coordinates only.
Let us further assume
that all off-diagonal matrix elements
indicates that the integration inside the braket is
over electronic coordinates only.
Let us further assume
that all off-diagonal matrix elements
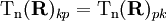 may be neglected except for k = 1 and
p = 2. Upon making the expansion
may be neglected except for k = 1 and
p = 2. Upon making the expansion
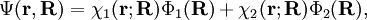
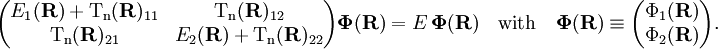
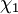 and
and 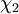
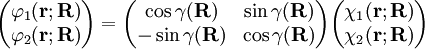
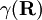 is the diabatic angle. Transformation of the matrix of nuclear momentum
is the diabatic angle. Transformation of the matrix of nuclear momentum 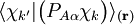 for
for 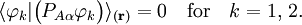
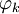 is real
and
is real
and 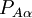 is Hermitian and pure-imaginary.
The off-diagonal elements of the momentum operator satisfy,
is Hermitian and pure-imaginary.
The off-diagonal elements of the momentum operator satisfy,
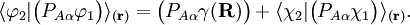
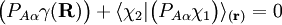
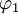 and
and 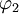 diagonalize the 2 x 2 matrix of the nuclear momentum. By the definition of
Smith
diagonalize the 2 x 2 matrix of the nuclear momentum. By the definition of
Smith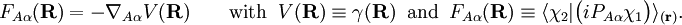
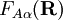 is irrotational,
is irrotational,

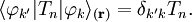
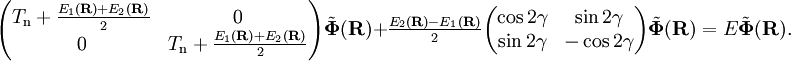
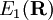 and
and 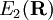 are adiabatic PESs obtained from clamped nuclei electronic structure calculations and
are adiabatic PESs obtained from clamped nuclei electronic structure calculations and 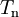 is the usual nuclear kinetic energy operator defined above.
Finding approximations for
is the usual nuclear kinetic energy operator defined above.
Finding approximations for