To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Molecular geometry
Molecular geometry or molecular structure is the three-dimensional arrangement of the atoms that constitute a molecule, inferred from the spectroscopic studies of the compound. It determines several properties of a substance including its reactivity, polarity, phase of matter, color, magnetism, and biological activity [1] [2]. Molecular geometries are best determined at temperatures close to absolute zero because at higher temperatures the molecules will show considerable rotational motion. In the solid state the molecular geometry can be measured by X-ray crystallography. Geometries can be computed by quantum mechanical calculations or by semi-empirical molecular modeling. Larger molecules often exist in multiple stable chemical conformations that differ in their molecular geometry and are separated by high hills in the potential energy surface. The position of each atom is determined by the nature of the chemical bonds by which it is connected to its neighboring atoms. The molecular geometry can be described by the positions of these atoms in space, evoking bond lengths of two joined atoms, bond angles of three connected atoms, and torsion angles of three consecutive bonds. Product highlight
The influence of thermal excitationSince the motions of the atoms in a molecule are determined by quantum mechanics, one must define “motion” in a quantum mechanical way. The overall (external) quantum mechanical motions translation and rotation hardly change the geometry of the molecule. (To some extent rotation influences the geometry via Coriolis forces and centrifugal distortion, but this is negligible for the present discussion.) A third type of motion is vibration, which is the internal motion of the atoms in a molecule. The molecular vibrations are harmonic (at least to good approximation), which means that the atoms oscillate about their equilibrium, even at the absolute zero of temperature. At absolute zero all atoms are in their vibrational ground state and show zero point quantum mechanical motion, that is, the wavefunction of a single vibrational mode is not a sharp peak, but an exponential of finite width. At higher temperatures the vibrational modes may be thermally excited (in a classical interpretation one expresses this by stating that “the molecules will vibrate faster”), but they oscillate still around the recognizable geometry of the molecule. To get a feeling for the probability that the vibration of molecule may be thermally excited,
we inspect the Boltzmann factor As stated above, rotation hardly influences the molecular geometry. But, as a quantum mechanical motion, it is thermally excited at relatively (as compared to vibration) low temperatures. From a classical point of view it can be stated that more molecules rotate faster at higher temperatures, i.e., they have larger angular velocity and angular momentum. In quantum mechanically language: more eigenstates of higher angular momentum become thermally populated with rising temperatures. Typical rotational excitation energies are on the order of a few cm-1. The results of many spectroscopic experiments are broadened because they involve an averaging over rotational states. It is often difficult to extract geometries from spectra at high temperatures, because the number of rotational states probed in the experimental averaging increases with increasing temperature. Thus, many spectroscopic observations can only be expected to yield reliable molecular geometries at temperatures close to absolute zero, because at higher temperatures too many higher rotational states are thermally populated. BondingMolecules, by definition, are most often held together with covalent bonds involving single, double, and/or triple bonds, where a "bond" is a shared pair of electrons (the other method of bonding between atoms is called ionic bonding and involves a positive cation and a negative anion). Molecular geometries can be specified in terms of bond lengths, bond angles and torsional angles. The bond length is defined to be the average distance between the centers of two atoms bonded together in any given molecule. A bond angle is the angle formed by three atoms bonded together. For four atoms bonded together in a straight chain, the torsional angle is the angle between the plane formed by the first three atoms and the plane formed by the last three atoms. Molecular geometry is determined by the quantum mechanical behaviour of the electrons. Using the valence bond approximation this can be understood by the type of bonds between the atoms that make up the molecule. Before atoms interact to form a chemical bond, the atomic orbitals mix in a process called orbital hybridisation.The two most common types of bonds are Sigma bonds and Pi bonds. The geometry can also be understood by molecular orbital theory where the electrons are delocalised. An understanding of the wavelike behavior of electrons in atoms and molecules is the subject of quantum chemistry. IsomersIsomers are types of molecules that share a chemical formula but have different geometries, resulting in very different properties:
Types of molecular structureThere are six basic shape types for molecules
References
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Molecular_geometry". A list of authors is available in Wikipedia. |





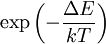 ,
where
,
where 

