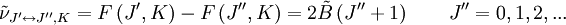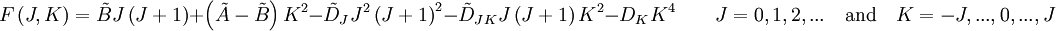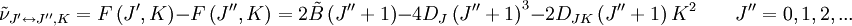To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Rotational spectroscopyRotational spectroscopy or microwave spectroscopy studies the absorption and emission electromagnetic radiation (typically in the microwave region of the electromagnetic spectrum) by molecules associated with a corresponding change in the rotational quantum number of the molecule. The use of microwaves in spectroscopy essentially became possible due to the development of microwave technology for RADAR during World War II. Rotational spectroscopy is only really practical in the gas phase where the rotational motion is quantized. In solids or liquids the rotational motion is usually quenched due to collisions. Rotational spectrum from a molecule (to first order) requires that the molecule have a dipole moment, that is a difference between the center of charge and the center of mass, or equivalently a separation between two unlike charges. It is this dipole moment that enables the electric field of the light (microwave) to exert a torque on the molecule causing it to rotate more quickly (in excitation) or slowly (in de-excitation). Diatomic molecules such as dioxygen (O2), dihydrogen (H2), etc. do not have a dipole moment and hence no purely rotational spectrum. However, electronic excitations can lead to asymmetric charge distributions and thus provide a net dipole moment to the molecule. Under such circumstances, these molecules will exhibit a rotational spectrum. Amongst the diatomic molecules, carbon monoxide (CO) has one of the simplest rotational spectra. As for tri-atomic molecules, hydrogen cyanide (HC≡N) has a simple rotational spectrum for a linear molecule and hydrogen isocyanide (HN=C:) for a non-linear molecule. As the number of atoms increases the spectrum becomes more complex as lines due to different transitions start overlapping. Product highlight
Understanding the rotational spectrumIn quantum mechanics the free rotation of a molecule is quantized, that is the rotational energy and the angular momentum can only take certain fixed values; what these values are is simply related to the moment of inertia, I, of the molecule. In general for any molecule, there are three moments of inertia: IA, IB and IC about three mutually orthogonal axes A, B, and C with the origin at the center of mass of the system. A linear molecule is a special case in this regard. These molecules are cylindrically symmetric and one of the moment of inertia (IA, which is the moment of inertia for a rotation taking place along the axis of the molecule) is negligible (i.e. IA < < IB = IC). Classification of molecules based on rotational behaviorThe general convention is to define the axes such that the axis A has the smallest moment of inertia (and hence the highest rotational frequency) and other axes such that IA < = IB < = IC. Sometimes the axis A may be associated with the symmetric axis of the molecule, if any. If such is the case, then IA need not be the smallest moment of inertia. To avoid confusion, we will stick with the former convention for the rest of the article. The particular pattern of energy levels (and hence of transitions in the rotational spectrum) for a molecule is determined by its symmetry. A convenient way to look at the molecules is to divide them into four different classes (based on the symmetry of their structure). These are,
Dealing with each in turn:
Structure of rotational spectrum
These molecules have two degenerate modes of rotation (IB = IC, IA = 0). Since we cannot distinguish between the two modes, we need only one rotational quantum number (J) to describe the rotational motion of the molecule. The rotational energy levels ( where Selection rules dictate that during emission or absorption the rotational quantum number has to change by unity i.e. where We observe that, for a rigid rotor, the transition lines are equally spaced in the wavenumber space. However, this is not always the case, except for the rigid rotor model. For non-rigid rotor model, we need to consider changes in the moment of inertia of the molecule. Two primary reasons for this are,
When a molecule rotates, the centrifugal force pulls the atoms apart. As a result, the moment of inertia of the molecule increases, thus decreasing where Accordingly the line spacing for the rotational mode changes to,
A molecule is always in vibration. As the molecule vibrates, its moment of inertia changes. Further there is a fictitious force, Coriolis coupling, between the vibrational motion of the nuclei in the rotating (non-inertial) frame. However, as long as the vibrational quantum number does not change (i.e. the molecule is in only one state of vibration), the effect of vibration on rotation are not important, because the time for vibration is much greater than the time required for rotation. The Coriolis coupling is often negligible, too, if one is interested in low vibrational and rotational quantum numbers only.
The rotational motion of a symmetric top molecule can be described by two independent rotational quantum numbers (since two axes have equal moments of inertia, the rotational motion about these axes requires only one rotational quantum number for complete description). Instead of defining the two rotational quantum numbers for two independent axes, we associate one of the quantum number (J) with the total angular momentum of the molecule and the other quantum number (K) with the angular momentum of the axis which has different moment of inertia (i.e. axis C for oblate symmetric top and axis A for prolate symmetric tops). The rotational energy where Selection rule for the these molecules provide the guidelines for possible transitions. Accordingly,
This is so because K is associated with the axis about which the molecule is symmetric and hence has no net dipole moment in that direction. Thus there is no interaction of this mode with the light particles (photon). This gives the transition wavenumbers of, which is the same as in the case of a linear molecule. In case of non-rigid rotors, the first order centrifugal distortion correction is given by, The suffixes on the centrifugal distortion constant D indicate the rotational mode involved and are not a function of the rotational quantum number. The location of the transition lines on a spectrum are given by,
Unlike other molecules, spherical top molecules have no net dipole moment, and hence they do not exhibit a pure rotational spectrum.
The spectrum for these molecules usually involves many lines due to three different rotational modes and their combinations. There is no general rule for studying the rotational spectrum of these molecules. Hyperfine interactions: In addition to the main structure that is observed in microwave spectra due to the rotational motion of the molecules, a whole host of further interactions are responsible for small details in the spectra, and the study of these details provides a very deep understanding of molecular quantum mechanics. The main interactions responsible for small changes in the spectra (additional splittings and shifts of lines) are due to magnetic and electrostatic interactions in the molecule. The particular strength of such interactions differs in different molecules, but in general, the order of these effects (in decreasing significance) is:
These interactions give rise to the characteristic energy levels that are probed in "magnetic resonance" spectroscopy such as NMR and ESR, where they represent the "zero field splittings" which are always present. Experimental determination of the spectrumFourier transform infrared (FTIR) spectroscopy can be used to experimentally study rotational spectrum. ApplicationsMicrowave spectroscopy is commonly used in physical chemistry to determine the structure of small molecules (such as ozone, methanol, or water) with high precision. Other common techniques for determining molecular structure, such as X-ray crystallography don't work very well for some of these molecules (especially the gases) and are not as precise. However, microwave spectroscopy is not useful for determining the structures of large molecules such as proteins. References
See also
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Rotational_spectroscopy". A list of authors is available in Wikipedia. |





 ) of the molecule based on
) of the molecule based on 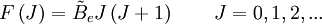
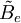 is the rotational constant of the molecule and is related to the moment of inertia of the molecule
is the rotational constant of the molecule and is related to the moment of inertia of the molecule 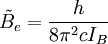
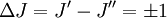 . Thus the locations of the lines in a rotational spectrum will be given by,
. Thus the locations of the lines in a rotational spectrum will be given by,
 denotes the lower energy level and
denotes the lower energy level and  denotes higher energy level involved in the transition. The height of the lines is determined by the distribution of the molecules in the different levels and the probability of transition between two energy levels.
denotes higher energy level involved in the transition. The height of the lines is determined by the distribution of the molecules in the different levels and the probability of transition between two energy levels.
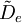 is the centrifugal distortion constant.
is the centrifugal distortion constant.
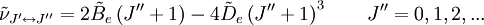
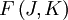 of such a molecule, based on
of such a molecule, based on 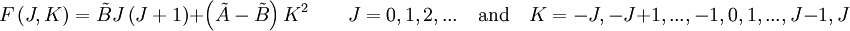
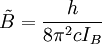 and
and 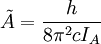 for a prolate symmetric top molecule or
for a prolate symmetric top molecule or
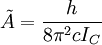 for an oblate molecule.
for an oblate molecule.
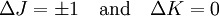 .
.