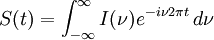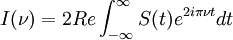To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Fourier transform spectroscopyFourier transform spectroscopy is a measurement technique whereby spectra are collected based on measurements of the temporal coherence of a radiative source, using time-domain measurements of the electromagnetic radiation or other type of radiation. It can be applied to a variety of types of spectroscopy including optical spectroscopy, infrared spectroscopy (IR), nuclear magnetic resonance, and electron spin resonance spectroscopy. There are several methods for measuring the temporal coherence of the light, including the continuous wave Michelson or Fourier transform spectrometer and the pulsed Fourier transform spectrograph (which is more sensitive and has a much shorter sampling time than conventional spectroscopic techniques, but is only applicable in a laboratory environment). Product highlight
Continuous wave Michelson or Fourier transform spectrograph
The Michelson spectrograph relies on the same principle as the Michelson-Morley experiment. Light from the source is split into two beams by a half-silvered mirror, one is reflected off a fixed mirror and one off a moving mirror which introduces a time delay -- the Fourier transform spectrometer is just a Michelson interferometer with a movable mirror. The beams interfere, allowing the temporal coherence of the light to be measured at each different time delay setting. By making measurements of the signal at many discrete positions of the moving mirror, the spectrum can be reconstructed using a Fourier transform of the temporal coherence of the light. Michelson spectrographs are capable of very high spectral resolution observations of very bright sources. The Michelson or Fourier transform spectrograph was popular for infra-red applications at a time when infra-red astronomy only had single pixel detectors. Imaging Michelson spectrometers are a possibility, but in general have been supplanted by imaging Fabry-Perot instruments which are easier to construct. Pulsed Fourier transform spectrometerA pulsed Fourier transform spectrometer is usually used to measure the spectrum of the light transmitted through a laboratory sample. In a conventional (or "continuous wave") spectrometer, a sample is exposed to electromagnetic radiation and the response (usually the intensity of transmitted radiation) is monitored. The energy of the radiation is varied over the desired range and the response is plotted as a function of radiation energy (or frequency). At certain resonant frequencies characteristic of the specific sample, the radiation will be absorbed resulting in a series of peaks in the spectrum, which can then be used to identify the sample. (In magnetic spectroscopy, the magnetic field is often varied instead of the frequency of the incident radiation, though the spectra are effectively the same as if the field had been kept constant and the frequency varied. This is largely a question of experimental convenience.) Instead of varying the energy of the electromagnetic radiation, Fourier Transform spectroscopy exposes the sample to a single pulse of radiation and measures the response. The resulting signal, called a free induction decay, is a direct measurement of the temporal coherence of the light and contains a rapidly decaying composite of all possible frequencies. Using a Fourier transform of this, the spectrum of the light can be calculated as for the Michelson Fourier transform spectrometer. In this way the Fourier transform spectrometer can produce the same kind of spectrum as a conventional spectrometer, but in a much shorter time. The principles of the Fourier transform approach can be compared to the behavior of a musical tuning fork. If a tuning fork is exposed to sound waves of varying frequencies, it will vibrate when the sound wave frequencies are in "tune". This is similar to conventional spectroscopic techniques, where the radiation frequency is varied and those frequencies where the sample is in "tune" with the radiation detected. However, if we strike the tuning fork (the equivalent of applying a pulse of radiation), the tuning fork will tend to vibrate at its characteristic frequencies. The resulting tone consists of a combination of all of the characteristic frequencies for that tuning fork. Similarly the response from a sample exposed to a pulse of radiation is a signal consisting primarily of the characteristic frequencies for that sample. The Fourier transform is a mathematical technique for determining these characteristic frequencies from a single composite signal. Multi-bounceA multi-bounce attenuated total reflectance (ATR) crystal makes it possible to increase the signal, facilitating surface analysis. Fellgett AdvantageOne of the most important advantages of FTS was shown by P.B. Fellgett, an early advocate of the method. The Fellgett advantage, also known as the multiplex principle, states that a multiplex spectrometer such as the FTS will produce a gain of the order of the square root of m in the signal-to-noise ratio of the resulting spectrum, when compared with an equivalent scanning monochromator, where m is the number of elements comprising the resulting spectrum when the measurement noise is dominated by detector noise. Converting spectra from time domain to frequency domainThe sum is performed over all contributing frequencies to give a signal S(t) in the time domain. gives non-zero value when S(t) contains a component that matches the oscillating function. References and notesFurther reading
See also
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Fourier_transform_spectroscopy". A list of authors is available in Wikipedia. |