To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Molecular vibration
A molecular vibration is excited when the molecule absorbs a quantum of energy, E, corresponding to the vibration's frequency, ν, according to the well-known relation E=hν, where h is Planck's constant. A fundamental vibration is excited when one such quantum of energy is absorbed by the molecule in its ground state. When two quanta are absorbed the first overtone is excited, and so on to higher overtones. To a first approximation, the motion in a normal vibration can be described as a kind of simple harmonic motion. In this approximation, the vibrational energy is a quadratic function (parabola) with respect to the atomic displacements and the first overtone would have twice the frequency of the fundamental. In reality, vibrations are anharmonic and the first overtone has a frequency that is slightly lower than twice that of the fundamental. Excitation of the higher overtones involves progressively less and less additional energy and eventually leads to dissociation of the molecule, as the potential energy of the molecule is more like a Morse potential. The vibrational states of a molecule can be probed in a variety of ways. The most direct way is through infrared spectroscopy, as vibrational transitions typically require an amount of energy that corresponds to the infrared region of the spectrum. Raman spectroscopy, which typically uses visible light, can also be used to measure vibration frequencies directly. Vibrational excitation can occur in conjunction with electronic excitation (vibronic transition), giving vibrational fine structure to electronic transitions, particularly with molecules in the gas state. Simultaneous excitation of a vibration and rotations gives rise to vibration-rotation spectra. Product highlight
Vibrational coordinatesThe coordinate of a normal vibration is a combination of changes in the positions of atoms in the molecule. When the vibration is excited the coordinate changes sinusoidally with a frequency ν, the frequency of the vibration. Internal coordinatesInternal coordinates are of the following types, illustrated with reference to the planar molecule ethene,
In a rocking, wagging or twisting coordinate the angles and bond lengths within the groups involved do not change. Rocking may be distinguished from wagging by the fact that the atoms in the group stay in the same plane. In ethene there are 12 internal coordinates: 4 C-H stretching, 1 C-C stretching, 2 H-C-H bending, 2 CH2 rocking, 2 CH2 wagging, 1 twisting. Note that the H-C-C angles cannot be used as internal coordinates as the angles at each carbon atom cannot all increase at the same time. See infrared spectroscopy for some animated illustrations of internal coordinates. Symmetry-adapted coordinatesSymmetry-adapted coordinates may be created by applying a projection operator to a set of internal coordinates.[1] The projection operator is constructed with the aid of the character table of the molecular point group. For example, the four(un-normalised) C-H stretching coordinates of the molecule ethene are given by
where q1 - q4 are the internal coordinates for stretching of each of the four C-H bonds. Illustrations of symmetry-adapted coordinates for most small molecules can be found in Nakamoto.[2] Normal coordinatesA normal coordinate, Q, may sometimes be constructed directly as a symmetry-adapted coordinate. This is possible when the normal coordinate belongs uniquely to a particular irreducible representation of the molecular point group. For example, the symmetry-adapted coordinates for bond-stretching of the linear carbon dioxide molecule, O=C=O are both normal coordinates:
The coefficients a and b are found by performing a full normal coordinate analysis by means of the Wilson GF method.[3] Newtonian mechanicsPerhaps surprisingly, molecular vibrations can be treated using Newtonian mechanics, to calculate the correct vibration frequencies. The basic assumption is that each vibration can be treated as though it corresponds to a spring. In the harmonic approximation the spring obeys Hooke's law: the force required to extend the spring is proportional to the extension. The proportionality constant is known as a force constant, f. The anharmonic oscillator is considered elsewhere.[4] By Newton’s second law of motion this force is also equal to a "mass", m, times acceleration. Since this is one and the same force the ordinary differential equation follows. The solution to this equation of simple harmonic motion is A is the maximum amplitude of the vibration coordinate Q. It remains to define the "mass", m. In a homonuclear diatomic molecule such as N2 it is simply the mass of the two atoms. In a heteronuclear diatomic molecule, AB, it is the reduced mass, μ given by The use of the reduced mass ensures that the centre of mass of the molecule is not affected by the vibration. In the harmonic approximation the potential energy of the molecule is a quadratic function of the normal coordinate. It follows that the force-constant is equal to the second derivative of the potential energy. When two or more normal vibrations have the same symmetry a full normal coordinate analysis must be performed (see GF method). The vibration frequencies,νi are obtained from the eigenvalues,λi, of the matrix product GF. G is a matrix of numbers derived from the masses of the atoms and the geometry of the molecule.[3] F is a matrix derived from force-constant values. Details concering the determination of the eigenvalues can be found in [5]. Quantum mechanicsIn the harmonic approximation the potential energy is a quadratic function of the normal coordinates. Solving the Schrödinger wave equation, the energy states for each normal coordinate are given by
where n is a quantum number that can take values of 0, 1, 2 ... The difference in energy when n changes by 1 are therefore equal to the energy derived using classical mechanics. See quantum harmonic oscillator for graphs of the first 5 wave functions. Knowing the wave functions, certain selection rules can be formulated. For example, for a harmonic oscillator transitions are allowed only when the quantum number n changes by one, but this does not apply to an anharmonic oscillator; the observation of overtones is only possible because vibrations are anharmonic. Another consequence of anharmonicity is that transitions such as between states n=2 and n=1 have slightly less energy than transitions between the ground state and first excited state. Such a transition gives rise to a hot band. IntensitiesIn an infrared spectrum the intensity of an absorption band is proportional to the devative of the molecular dipole moment with respect to the normal coordinate.[6] The intensity of Raman bands depends on polarizability. See also transition dipole moment. References
See also
Further reading
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Molecular_vibration". A list of authors is available in Wikipedia. |





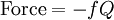
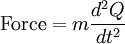
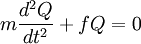
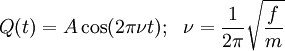
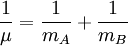
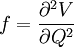
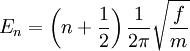 ,
,