To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Resonance Raman spectroscopyResonance Raman (RR) spectroscopy is a specialized implementation of the more general Raman spectroscopy. Product highlight
OverviewAs in Raman spectroscopy, RR spectroscopy provides information about the vibrations of molecules, and can also be used for identifying unknown substances. RR spectroscopy has found wide application to the analysis of bioinorganic molecules. Although the technique uses a different part of the electromagnetic spectrum than infrared (IR) spectroscopy, the two methods are actually complementary. Both are used to measure the energy required to change the vibrational state of a chemical compound. IR spectroscopy involves measuring the direct absorption of photons with the appropriate energy to excite molecular bond vibrations. The wavelengths of these photons lie in the infrared region of the spectrum, hence the name of the technique. Raman spectroscopy measures the excitation of bond vibrations in an indirect manner. The two methods are complementary because some vibrational transitions that are observed in IR spectroscopy are not observed in Raman spectroscopy, and vice versa. RR spectroscopy is an improvement of traditional Raman spectroscopy that has increased sensitivity and is better suited for the study of complicated systems. X-Ray Raman Scattering In the x-ray region, enough energy is available for making electronic transitions possible. At core level resonances, X-Ray Raman Scattering can become the dominating part of the x-ray fluorescence spectrum. This is due to the resonant behavior of the Kramers-Heisenberg formula in which the denominator is minimized for incident energies that equal a core level. This type of scattering is also known as resonant inelastic x-ray scattering (RIXS). In the soft x-ray range, RIXS has been shown to reflect crystal field excitations, which are often hard to observe with any other technique. Application of RIXS to strongly correlated materials is of particular value for gaining knowledge about their electronic structure. For certain wide band materials such as graphite, RIXS has been shown to (nearly) conserve crystal momentum and thus has found use as a complementary bandmapping technique. HistoryRaman spectroscopy utilizes the phenomenon of scattering. When light passes through a transparent sample, a fraction of the light is scattered in all directions. Most of the scattered photons are of the same wavelength of the incident light. This is known as Rayleigh scattering. However, in 1928, physicists C.V. Raman and K.S. Krishnan, and independently Grigory Landsberg and Leonid Mandelstam discovered that a small fraction of the scattered light had a different wavelength. Furthermore, this difference depended on the molecules present in the sample. For these observations, and his explanation of the phenomenon, Raman was awarded the 1930 Nobel Prize in physics. His explanation is now known as the theory of Raman scattering. In the years following its discovery, Raman spectroscopy was used to provide the first catalog of molecular vibrational frequencies. Originally, heroic measures were required to obtain Raman spectra due to the low sensitivity of the technique. Typically, the sample was held in a long tube and illuminated along its length with a beam of filtered monochromatic light generated by a gas discharge lamp. The photons that were scattered by the sample were collected through an optical flat at the end of the tube. To maximize the sensitivity, the sample was highly concentrated (1 M or more) and relatively large volumes (5 mL or more) were used. Consequently, the use of Raman spectroscopy dwindled when commercial IR spectrophotometers became available in the 1940s. However, the advent of the laser in the 1960s resulted in simplified Raman spectroscopy instruments and also boosted the sensitivity of the technique. This has revived the use of Raman spectroscopy as a common analytical technique. Theory of Raman ScatteringDegrees of FreedomFor any given chemical compound, there are a total of 3N degrees of freedom, where N is the number of atoms in the compound. This number arises from the ability of each atom in a molecule to move in three different directions (x, y, and z). When dealing with molecules, it is more common to consider the movements of the molecule as a whole. Consequently, the 3N degrees of freedom are partitioned into molecular translational, rotational, and vibrational motion. Three of degrees of freedom correspond to translational movement of the molecule as a whole (along each of the three spatial dimensions). Similarly, three degrees of freedom correspond to rotations of the molecule about the x, y, and z-axes. However, linear molecules only have two rotations because rotations along the bond axis do not change the positions of the atoms in the molecule. The remaining degrees of freedom correspond to molecular vibrational modes. These modes include stretching and bending motions of the chemical bonds of the molecule. For a linear molecule, the number of vibrational modes is: 3N − 3 − 2 = 3N − 5 whereas for a non-linear molecule the number of vibrational modes are 3N − 6 Molecular Vibrations and Infrared RadiationThe frequencies of molecular vibrations are in the range of 1012 to 1014 Hz. These frequencies correspond to radiation in the infrared (IR) region of the electromagnetic spectrum. At any given instant, each molecule in a sample has a certain amount of vibrational energy. However, the amount of vibrational energy that a molecule has continually changes due to collisions and other interactions with other molecules in the sample. At room temperature, most of molecules will be in the lowest energy state, which is known as the ground state. A few molecules will be in higher energy states, which are known as excited states. The fraction of molecules occupying a given vibrational mode at a given temperature can be calculated using the Boltzmann distribution. Performing such a calculation shows that, for relatively low temperatures (such as those used for most routine spectroscopy), most of the molecules occupy the ground vibrational state. Such a molecule can be excited to a higher vibrational mode through the direct absorption of a photon of the appropriate energy. This is the mechanism by which IR spectroscopy operates: infrared radiation is passed through the sample, and the intensity of the transmitted light is compared with that of the incident light. A reduction in intensity at a given wavelength of light indicates the absorption of energy by a vibrational transition. The energy, E, of a photon is E = hν where h is Planck’s constant and ν is the frequency of the radiation. Thus, the energy required for such transition may be calculated if the frequency of the incident radiation is known. Raman ScatteringIt is also possible to observe molecular vibrations by an inelastic scattering process. In inelastic scattering, an absorbed photon is re-emitted with lower energy. In Raman scattering, the difference in energy between the absorbed and re-emitted photons corresponds to the energy required to excite a molecule to a higher vibrational mode. Typically, in Raman spectroscopy high intensity laser radiation with wavelengths in either the visible or near-infrared regions of the spectrum is passed through a sample. Photons from the laser beam are absorbed by the molecules, exciting them to a virtual energy state. If the molecules relax back to the vibrational state that they started in, the reemitted photon has the same energy as the original photon. This leads to scattering of the laser light, but with no change in energy between the incoming photons and the reemitted/scattered photons. This type of scattering is known as Rayleigh scattering. However, it is possible for the molecules to relax back to a vibrational state that is higher in energy than the state they started in. In this case, the original photon and the reemitted photon differ in energy by the amount required to vibrationally excite the molecule. Generally, the difference in energy is recorded as the difference in wavenumber ( A Raman spectrum also exhibits peaks that correspond to negative values of Resonance Raman SpectroscopyRaman spectroscopy can be used to identify chemical compounds because the values of Not all vibrational transitions will be “Raman active”, i.e. some vibrational transitions will not appear in the Raman spectrum. This is because of the spectroscopic selection rules for Raman. As opposed to IR spectroscopy, where a transition can only be seen when that particular vibration causes a net change in dipole moment of the molecule, in Raman only transitions where the polarizability of the molecule changes can be observed. This is due to the fundamental difference in how IR and Raman spectroscopy access the vibrational transitions. In Raman spectroscopy, the incoming photon causes a momentary distortion of the electron distribution around a bond in a molecule, followed by reemission of the radiation as the bond returns to its normal state. This causes temporary polarization of the bond, and an induced dipole that disappears upon relaxation. In a molecule with a center of symmetry, a change in dipole is accomplished by loss of the center of symmetry, while a change in polarizability is accomplished by preservation of the center of symmetry. Thus, in a centrosymmetric molecule, asymmetrical stretching and bending will be IR active and Raman inactive, while symmetrical stretching and bending will be Raman active and IR inactive. Hence, in a centrosymmetric molecule, IR and Raman spectroscopy are mutually exclusive. For molecules without a center of symmetry, each vibrational mode may be IR active, Raman active, both, or neither. Symmetrical stretches and bends, however, tend to be Raman active. In resonance Raman spectroscopy, the energy of the incoming laser energy is adjusted such that it or the scattered light coincide with an electronic transition of the molecule or crystal. In most materials the incoming and outgoing electronic resonances are sufficiently broad that they can not be distinguished. So, rather than exciting the molecule to a virtual energy state, it is excited to near one of its excited electronic transitions. Since the energy of these transitions differ from one chemical species to the next, this technique did not become applicable until the advent of tunable lasers in the early 1970s. (Tunable lasers are those where the wavelength can be altered within a specific range.) When the frequency of the laser beam is tuned to be near an electronic transition (resonance), the vibrational modes associated with that particular transition exhibit a greatly increased Raman scattering intensity. This usually overwhelms Raman signals from all of the other transitions. For instance, resonance with a π-π* transition enhances stretching modes of the π-bonds involved with the transition, while the other modes remain unaffected. This aspect of Raman spectroscopy becomes especially useful for large biomolecules with chromophores embedded in their structure. In such chromophores, the charge-transfer (CT) transitions of the metal complex generally enhance metal-ligand stretching modes, as well as some of modes associated with the ligands alone. Hence, in a biomolecule such as hemoglobin, tuning the laser to near the charge-transfer electronic transition of the iron center results in a spectrum reflecting only the stretching and bending modes associated with the tetrapyrrole-iron group. Consequently, in a molecule with thousands of vibrational modes, RR spectroscopy allows us to look at relatively few vibrational modes at a time. This reduces the complexity of the spectrum and allows for easier identification of an unknown protein. Also, if a protein has more than one chromophore, different chromophores can be studied individually if their CT bands differ in energy. In addition to identifying compounds, RR spectroscopy can also supply structural identification about chromophores in some cases. The main advantage of RR spectroscopy over traditional Raman spectroscopy is the large increase in intensity of the peaks in question (by as much as a factor of 106). This allows RR spectra to be generated with sample concentrations as low as 10-8 M. This is in stark contrast to conventional Raman spectra, which usually requires concentrations greater than 0.01 M. Also, as previously mentioned, RR spectra usually exhibit only a few peaks, and different peaks can be selected for by targeting specific electronic transitions. The main disadvantage of RR spectroscopy is the increased risk of fluorescence and photodegradation of the sample due to the increased energy of the incoming laser light. Both of these factors can be minimized by using an infrared laser instead of visible light. InstrumentationIn RR spectroscopy, the light source consists of a tunable laser, whose radiation lies in either the near-infrared, visible, or near-ultraviolet regions of the spectrum. In creating a sample handling system, RR spectroscopy offers an advantage over IR spectroscopy in that glass can be used for windows, lenses, and other optical components. Another advantage over IR spectroscopy is that whereas water absorbs strongly in the IR, it is completely Raman inactive. Therefore, water can easily be used as a solvent. Since lasers can be easily focused on small surface areas, the risk of sample heating and photodegradation is diminished, and the emitted radiation can be focused more efficiently. Typically, the sample is placed into a tube, which can then be spun to further decrease the sample’s exposure to the laser light, further diminishing the threat of photodegradation. Gaseous, liquid, and solid samples can all be analyzed using RR spectroscopy. Gas and liquid samples can be put directly into the sample chamber whereas solid samples must first be ground into a powder. With gaseous and solid samples, Raman scattering may still be too weak to easily detect. For these samples, the sample holder is placed between two mirrors that reflect the laser beam multiple times through the sample. Since scattered light leaves the sample in all directions the probes that carry the scattered light back to the detector in Raman spectroscopy may be placed at any angle. Usually, the detector probes are most placed at an angle of 135° to the path of the exiting laser light beam. Two other common arrangements position the detector probe at 90° or 180° with respect to the incident light. Detection angles greater than 90° are generally called back-scattering detectors because they are oriented in the same direction as the incident laser light so the radiation must scatter back to the probes. In transmitting the incident laser light to the sample and the scattered light back to the detector, fiber-optic cables may be used. Such cables can transmit light 100 m or more, thereby allowing the analysis of samples under relatively rough experimental/environmental conditions. After the scattered radiation exits the sample, it is sent through a monochromator. Typical monochromators consist of a diffraction grating mounted on a rotating platform. A diffraction grating causes light dispersion. Rotating the grating controls which wavelengths of scattered radiation reach the exit slit leading to the detector. The detector itself is usually a charge-coupled device (CCD), which allows the entire spectrum to be recorded simultaneously. Consequently, multiple scans can be acquired in a short period of time, which can drastically increase the signal-to-noise ratio of the spectrum. Currently, Raman spectrometers are more expensive than more traditional dispersive instruments. As the cost of tunable lasers decrease, RR spectroscopy should see increased use, especially in the studies of metal-ligand vibrations, which reside in a region that is typically very difficult to study by other instrumental techniques. With the advent of near-infrared tunable lasers, particularly the Ti-sapphire dye laser (which has a range of ~700-1100 nm), Fourier Transform Resonance Raman Spectrometers may soon be commercially available. These would offer the multiplex and Jaquinot advantages of Fourier Transform (FT) techniques. See also
References
Resources
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Resonance_Raman_spectroscopy". A list of authors is available in Wikipedia. |





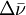 ) between the laser light and the scattered light. A Raman spectrum is generated by plotting the intensity of the reemitted light versus
) between the laser light and the scattered light. A Raman spectrum is generated by plotting the intensity of the reemitted light versus 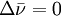 ). The anti-Stokes lines are appreciably less intense than the corresponding Stokes lines. This is because initially very few molecules are in excited vibrational states compared to the number in the ground state. Since anti-Stokes lines arise from the former and Stokes lines arise from the latter, the Stokes lines are much more intense. However, it should be noted that in molecules which exhibit
). The anti-Stokes lines are appreciably less intense than the corresponding Stokes lines. This is because initially very few molecules are in excited vibrational states compared to the number in the ground state. Since anti-Stokes lines arise from the former and Stokes lines arise from the latter, the Stokes lines are much more intense. However, it should be noted that in molecules which exhibit 

