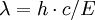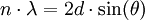To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
X-ray fluorescenceX-ray fluorescence (XRF) is the emission of characteristic "secondary" (or fluorescent) X-rays from a material that has been excited by bombarding with high-energy X-rays or gamma rays. The phenomenon is widely used for elemental analysis and chemical analysis, particularly in the investigation of metals, glass, ceramics and building materials, and for research in geochemistry, forensic science and archaeology. Product highlight
The physics of XRFWhen materials are exposed to short-wavelength x-rays or to gamma rays, ionization of their component atoms may take place. Ionization consists of the ejection of one or more electrons from the atom, and may take place if the atom is exposed to radiation with an energy greater than its ionization potential. X-rays and gamma rays can be energetic enough to expel tightly-held electrons from the inner orbitals of the atom. The removal of an electron in this way renders the electronic structure of the atom unstable, and electrons in higher orbitals "fall" into the lower orbital to fill the hole left behind. In falling, energy is released in the form of a photon, the energy of which is equal to the energy difference of the two orbitals involved. Thus, the material emits radiation, which has energy characteristic of the atoms present. The term fluorescence is applied to phenomena in which the absorption of higher-energy radiation results in the re-emission of lower-energy radiation.
Characteristic radiationEach element has electronic orbitals of characteristic energy. Following removal of an inner electron by an energetic photon provided by a primary radiation source, an electron from an outer shell drops into its place. There are a limited number of ways in which this can happen, as shown in figure 1. The main transitions are given names: an L→K transition is traditionally called Kα, an M→K transition is called Kβ, an M→L transition is called Lα, and so on. Each of these transitions yields a fluorescent photon with a characteristic energy equal to the difference in energy of the initial and final orbital. The wavelength of this fluorescent radiation can be calculated from Planck's Law:
The fluorescent radiation can be analyzed either by sorting the energies of the photons (energy-dispersive analysis) or by separating the wavelengths of the radiation (wavelength-dispersive analysis). Once sorted, the intensity of each characteristic radiation is directly related to the amount of each element in the material. This is the basis of a powerful technique in analytical chemistry. Figure 2 shows the typical form of the sharp fluorescent spectral lines obtained in the wavelength-dispersive method. Primary radiationIn order to excite the atoms, a source of radiation is required, with sufficient energy to expel tightly-held inner electrons. Conventional x-ray tubes are most commonly used, because their output can readily be "tuned" for the application, and because very high power can be deployed. However, gamma ray sources can be used without the need for an elaborate power supply, allowing use in small portable instruments. When the energy source is a synchrotron, or the X-ray are focussed by an optic, like a polycapillary, the X-ray beam can be very small and very intense, and atomic information on the sub-micrometer scale can be obtained. X-ray tubes are operated at a high voltage (typically in the range 20-60 kV) in order to obtain a more or less continuous spectrum, which allows excitation of a broad range of atoms. The continuous spectrum consists of "bremsstrahlung" radiation: radiation produced when high energy electrons passing through the tube are progressively decelerated by the material of the tube anode (the "target"). A typical tube output spectrum is shown in figure 3. DispersionIn energy dispersive analysis, the fluorescent x-rays emitted by the material sample are directed into a solid-state detector which produces a continuous distribution of pulses, the voltages of which are proportional to the incoming photon energies. This signal is processed by a multichannel analyzer (MCA) which produces an accumulating digital spectrum that can be processed to obtain analytical data. In wavelength dispersive analysis, the fluorescent x-rays emitted by the material sample are directed into a diffraction grating monochromator. The diffraction grating used is usually a single crystal. By varying the angle of incidence and take-off on the crystal, a single x-ray wavelength can be selected. The wavelength obtained is given by the Bragg Equation:
where d is the spacing of atomic layers parallel to the crystal surface. DetectionIn energy dispersive analysis, dispersion and detection are a single operation, as described above. In wavelength dispersive analysis, the single-wavelength radiation produced by the monochromator is passed into a detector similar to a Geiger counter, which counts individual photons as they pass through. The counter is a chamber containing a gas that is ionized by x-ray photons. A central electrode is charged at (typically) +1700 V with respect to the conducting chamber walls, and each photon triggers a pulse-like cascade of current across this field. The signal is amplified and transformed into an accumulating digital count. These counts are then processed to obtain analytical data. X-ray intensityThe fluorescence process is inefficient, and the secondary radiation is much weaker than the primary beam. Furthermore, the secondary radiation from lighter elements is of low energy (long wavelength) and has low penetrating power, and is severely attenuated if the beam passes through air for any distance. Because of this, for high-performance analysis, the path from tube to sample to detector is maintained under high vacuum (around 10 Pa residual pressure). This means in practice that most of the working parts of the instrument have to be located in a large vacuum chamber. The problems of maintaining moving parts in vacuo, and of rapidly introducing and withdrawing the sample without losing vacuum, pose major challenges for the design of the instrument. For less demanding applications, or when the sample is damaged by a vacuum (e.g. a volatile sample), a helium-swept x-ray chamber can be substituted, with some loss of low-Z intensities. XRF in chemical analysisThe use of a primary X-ray beam to excite fluorescent radiation from the sample was first proposed by Glocker and Schreiber in 1928[1]. Today, the method is used as a non-destructive analytical technique, and as a process control tool in many extractive and processing industries. In principle, the lightest element that can be analysed is beryllium (Z = 4), but due to instrumental limitations and low x-ray yields for the light elements, it is often difficult to quantify elements lighter than sodium (Z = 11), unless background corrections and very comprehensive interelement corrections are made.
Energy dispersive spectrometryIn energy dispersive spectrometers (EDX or EDS), the detector allows the determination of the energy of the photon when it is detected. Detectors historically have been based on silicon semiconductors, in the form of lithium-drifted silicon crystals, or high-purity silicon wafers.
Si(Li) detectorsThese consist essentially of a 3-5 mm thick silicon junction type p-i-n diode with a bias of -1000 v across it. The lithium-drifted centre part forms the non-conducting i-layer. When an x-ray photon passes through, it causes a swarm of electron-hole pairs to form, and this causes a voltage pulse. To obtain sufficiently low conductivity, the detector must be maintained at low temperature, and liquid-nitrogen must be used for the best resolution. With some loss of resolution, the much more convenient Peltier cooling can be employed. Wafer detectorsMore recently, high-purity wafer silicon with low conductivity has become routinely available. Cooled by the Peltier effect, this provides a cheap and convenient detector, although the liquid nitrogen cooled Si(Li) detector still has the best resolution (i.e. ability to distinguish different photon energies). AmplifiersThe pulses generated by the detector are processed by pulse-shaping amplifiers. It takes time for the amplifier to shape the pulse for optimum resolution, and there is therefore a trade-off between resolution and count-rate: long processing time for good resolution results in "pulse pile-up" in which the pulses from successive photons overlap, so that only very low count-rates can be used for linear performance. From the point of view of high-speed measurement, this is an important disadvantage of EDX. On the other hand, the low X-ray flux needed for low count-rates can readily be provided by cheap low-power x-ray sources or gamma sources. ProcessingConsiderable computer power is dedicated to correcting for pulse-pile up and for extraction of data from poorly-resolved spectra. These elaborate correction processes tend to be based on empirical relationships that may change with time, so that continuous vigilance is required in order to obtain chemical data of adequate precision. UsageEDX spectrometers compare favorably with WDX spectrometers in that they can be smaller, simpler in design and have fewer engineered parts. They can also use miniature X-ray tubes or gamma sources. This makes them cheaper and allows miniaturization and portability. This type of instrument is commonly used for portable quality control screening applications, such as testing toys for Lead (Pb) content, sorting scrap metals, and measuring the lead content of residential paint. On the other hand, the low resolution and problems with low count rate and long dead-time makes them inferior for high-precision and high-speed analysis. Field Portable XRF analyzers currently on the market weigh less than 2 kg, and have limits of detection on the order of 2 parts per million of Lead (Pb) in pure sand.
Wavelength dispersive spectrometryIn wavelength dispersive spectrometers (WDX or WDS), the photons are separated by diffraction on a single crystal before being detected. Although wavelength dispersive spectrometers are occasionally used to scan a wide range of wavelengths, producing a spectrum plot as in EDS, they are usually set up to make measurements only at the wavelength of the emission lines of the elements of interest. This is achieved in two different ways:
Sample presentationIn order to keep the geometry of the tube-sample-detector assembly constant, the sample is normally prepared as a flat disc, typically of diameter 20-50 mm. This is located at a standardized, small distance from the tube window. Because the X-ray intensity follows an inverse-square law, the tolerances for this placement and for the flatness of the surface must be very tight in order to maintain a repeatable X-ray flux. Ways of obtaining sample discs vary: metals may be machined to shape, minerals may be finely ground and pressed into a tablet, and glasses may be cast to the required shape. A further reason for obtaining a flat and representative sample surface is that the secondary X-rays from lighter elements often only emit from the top few micrometers of the sample. In order to further reduce the effect of surface irregularities, the sample is usually spun at 5-20 rpm. It is necessary to ensure that the sample is sufficiently thick to absorb the entire primary beam. For higher-Z materials, a few millimeters thickness is adequate, but for a light-element matrix such as coal, a thickness of 30-40 mm is needed.
MonochromatorsThe common feature of monochromators is the maintenance of a symmetrical geometry between the sample, the crystal and the detector. In this geometry the Bragg diffraction condition is obtained. The X-ray emission lines are very narrow (see figure 2), so the angles must be defined with considerable precision. This is achieved in two ways:
The Soller collimator is a stack of parallel metal plates, spaced a few tenths of a millimeter apart. To improve angle resolution, one must lengthen the collimator, and/or reduce the plate spacing. This arrangement has the advantage of simplicity and relatively low cost, but the collimators reduce intensity and increase scattering, and reduce the area of sample and crystal that can be "seen". The simplicity of the geometry is especially useful for variable-geometry monochromators.
The Rowland circle geometry ensures that the slits are both in focus, but in order for the Bragg condition to be met at all points, the crystal must first be bent to a radius of 2R (where R is the radius of the Rowland circle), then ground to a radius of R. This arrangement allows higher intensities (typically 8-fold) with higher resolution (typically 4-fold) and lower background. But the mechanics of keeping Rowland circle geometry in a variable-angle monochromator is extremely difficult. In the case of fixed-angle monochromators (for use in simultaneous spectrometers), crystals bent to a logarithmic spiral shape give the best focusing performance. The manufacture of curved crystals to acceptable tolerances increases their price considerably. Analysis LinesThe spectral lines used for chemical analysis are selected on the basis of intensity, accessibility by the instrument, and lack of line overlaps. Typical lines used, and their wavelengths, are as follows:
Other lines are often used, depending on the type of sample and equipment available. CrystalsThe desirable characteristics of a diffraction crystal are:
Crystals with simple structure tend to give the best diffraction performance. Crystals containing heavy atoms can diffract well, but also fluoresce themselves, causing interference. Crystals that are water-soluble, volatile or organic tend to give poor stability. Commonly used crystal materials include LiF (lithium fluoride), ADP (ammonium dihydrogen phosphate), Ge (germanium), graphite, InSb (indium antimonide), PE (tetrakis-(hydroxymethyl)-methane: penta-erythritol), KAP (potassium hydrogen phthalate), RbAP (rubidium hydrogen phthalate) and TlAP (thallium(I) hydrogen phthalate). In addition, there is an increasing use of "layered synthetic microstructures", which are "sandwich" structured materials comprising successive thick layers of low atomic number matrix, and monoatomic layers of a heavy element. These can in principle be custom-manufactured to diffract any desired long wavelength, and are used extensively for elements in the range Li to Mg. Properties of commonly used crystals
DetectorsDetectors used for wavelength dispersive spectrometry need to have high pulse processing speeds in order to cope with the very high photon count rates that can be obtained. In addition, they need sufficient energy resolution to allow filtering-out of background noise and spurious photons from the primary beam or from crystal fluorescence. There are four common types of detector:
Gas flow proportional counters are used mainly for detection of longer wavelengths. Gas flows through it continuously. Where there are multiple detectors, the gas is passed through them in series, then led to waste. The gas is usually 90% argon, 10% methane ("P10"), although the argon may be replaced with neon or helium where very long wavelengths (over 5 nm) are to be detected. The argon is ionized by incoming X-ray photons, and the electric field multiplies this charge into a measurable pulse. The methane suppresses the formation of fluorescent photons caused by recombination of the argon ions with stray electrons. The anode wire is typically tungsten or nichrome of 20-60 μm diameter. Since the pulse strength obtained is essentially proportional to the ratio of the detector chamber diameter to the wire diameter, a fine wire is needed, but it must also be strong enough to be maintained under tension so that it remains precisely straight and concentric with the detector. The window needs to be conductive, thin enough to transmit the X-rays effectively, but thick and strong enough to minimize diffusion of the detector gas into the high vacuum of the monochromator chamber. Materials often used are beryllium metal, aluminized Mylar and aluminized polypropylene. Ultra-thin windows (down to 1 μm) for use with low-penetration long wavelengths are very expensive. The pulses are sorted electronically by "pulse height selection" in order to isolate those pulses deriving from the secondary X-ray photons being counted. Sealed gas detectors are similar to the gas flow proportional counter, except that the gas does not flow though it. The gas is usually krypton or xenon at a few atmospheres pressure. They are applied usually to wavelengths in the 0.15-0.6 nm range. They are applicable in principle to longer wavelengths, but are limited by the problem of manufacturing a thin window capable of withstanding the high pressure difference. Scintillation counters consist of a scintillating crystal (typically of sodium iodide doped with thallium) attached to a photomultiplier. The crystal produces a group of scintillations for each photon absorbed, the number being proportional to the photon energy. This translates into a pulse from the photomultiplier of voltage proportional to the photon energy. The crystal must be protected with a relatively thick aluminium/beryllium foil window, which limits the use of the detector to wavelengths below 0.25 nm. Scintillation counters are often connected in series with a gas flow proportional counter: the latter is provided with an outlet window opposite the inlet, to which the scintillation counter is attached. This arrangement is particularly used in sequential spectrometers. Semiconductor detectors can be used in theory, and their applications are increasing as their technology improves, but historically their use for WDX has been restricted by their slow response (see EDX).
Extracting analytical resultsAt first sight, the translation of X-ray photon count-rates into elemental concentrations would appear to be straightforward: WDX separates the X-ray lines efficiently, and the rate of generation of secondary photons is proportional to the element concentration. However, the number of photons leaving the sample is also affected by the physical properties of the sample: so-called "matrix effects". These fall broadly into three categories:
All elements absorb X-rays to some extent. Each element has a characteristic absorption spectrum which consists of a "saw-tooth" succession of fringes, each step-change of which has wavelength close to an emission line of the element. Absorption attenuates the secondary X-rays leaving the sample. For example, the mass absorption coefficient of silicon at the wavelength of the aluminium Kα line is 50 m²/kg, whereas that of iron is 377 m²/kg. This means that a given concentration of aluminium in a matrix of iron gives only one seventh of the countrate compared with the same concentration of aluminium in a silicon matrix. Fortunately, mass absorption coefficients are well known and can be calculated. However, to calculate the absorption for a multi-element sample, the composition must be known. For analysis of an unknown sample, an iterative procedure is therefore used. It will be noted that, to derive the mass absorption accurately, data for the concentration of elements not measured by XRF may be needed, and various strategies are employed to estimate these. As an example, in cement analysis, the concentration of oxygen (which is not measured) is calculated by assuming that all other elements are present as standard oxides. Enhancement occurs where the secondary X-rays emitted by a heavier element are sufficiently energetic to stimulate additional secondary emission from a lighter element. This phenomenon can also be modeled, and corrections can be made provided that the full matrix composition can be deduced. Sample macroscopic effects consist of effects of inhomogeneities of the sample, and unrepresentative conditions at its surface. Samples are ideally homogenous and isotropic, but they often deviate from this ideal. Mixtures of multiple crystalline components in mineral powders can result in absorption effects that deviate from those calculable from theory. When a powder is pressed into a tablet, the finer minerals concentrate at the surface. Spherical grains tend to migrate to the surface more than do angular grains. In machined metals, the softer components of an alloy tend to smear across the surface. Considerable care and ingenuity are required to minimize these effects. Because they are artifacts of the method of sample preparation, these effects can not be compensated by theoretical corrections, and must be "calibrated in". This means that the calibration materials and the unknowns must be compositionally and mechanically similar, and a given calibration is applicable only to a limited range of materials. Glasses most closely approach the ideal of homogeneity and isotropy, and for accurate work, minerals are usually prepared by dissolving them in a borate glass, and casting them into a flat disc or "bead". Prepared in this form, a virtually universal calibration is applicable. Further corrections that are often employed include background correction and line overlap correction. The background signal in an XRF spectrum derives primarily from scattering of primary beam photons by the sample surface. Scattering varies with the sample mass absorption, being greatest when mean atomic number is low. When measuring trace amounts of an element, or when measuring on a variable light matrix, background correction becomes necessary. This is really only feasible on a sequential spectrometer. Line overlap is a common problem, bearing in mind that the spectrum of a complex mineral can contain several hundred measurable lines. Sometimes it can be overcome by measuring a less-intense, but overlap-free line, but in certain instances a correction is inevitable. For instance, the Kα is the only usable line for measuring sodium, and it overlaps the zinc Lβ (L2-M4) line. Thus zinc, if present, must be analyzed in order to properly correct the sodium value. Other spectroscopic methods using the same principleIt is also possible to create a characteristic secondary X-ray emission with other incident radiation to excite the sample:
When radiated by an X-ray beam, the sample also emits other radiations that can be used for analysis:
The de-excitation also gives ejection of Auger electrons, but the Auger electron spectroscopy (AES) uses an electron beam as primary beam. See also
Notes
References
Categories: Atomic physics | Molecular physics | Spectroscopy | X-rays |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "X-ray_fluorescence". A list of authors is available in Wikipedia. |