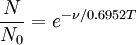Hot transition

In molecular vibrations a hot transition is a transition between two states of a single normal mode of vibration, neither of which is the ground state^[1] When observed in infrared or Raman spectroscopy it is known as a hot band. In the harmonic approximation hot transitions are forbidden by selection rule but as all vibrations are anharmonic to some extent hot transitions are weakly allowed. Because of anharmonicity, the frequency of a hot band is less than the frequency of the corresponding fundamental. The frequency difference depends on the magnitude of the anharmonic terms in the potential energy.

Additional recommended knowledge

Safe Weighing Range Ensures Accurate Results

How to quickly check pipettes?

Weighing the right way

Both the lower and upper states involved in the transition are excited states. Therefore an excited state must be populated for a hot band to be observed. The most common form of excitation is by thermal energy. The population of the excited state is then given by the Boltzmann distribution. In simplified form this can be expressed as

where ν is the frequency /cm^-1 of the hot band and T is the temperature /K. Thus, the intensity of a hot band, which is proportional to the population of the excited state , increases as the temperature increases. Hot bands are more likely to be observed with low-frequency vibrations than with high-frequency vibrations.

Difference transition

A difference transition occurs between excited states of two different vibrations. The frequency of a difference band is approximately equal to the difference between the fundamental frequencies. The difference is not exact because there is anharmonicity in both vibrations.

The intensity of a hot band or a difference band is generally rather low compared to the intensity of the fundamental band(s) both because they are harmonic-forbidden and because the excited state population is low.

Sum transition

A sum transition occurs when two fundamental vibrations are excited simultaneously. The frequency of a sum band is slightly less than the sum of the frequencies of the fundamentals.

A sum band will have low intensity because it is harmonic-forbidden but the intensity is greater than that of the corresponding difference band.

Both sum and difference bands are examples of combination bands.

References

1. ^ S. Califano, Vibrational States, Wiley, 1976