To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Morse potential
The Morse potential, named after physicist Philip M. Morse, is a convenient model for the potential energy of a diatomic molecule. It is a better approximation for the vibrational structure of the molecule than the quantum harmonic oscillator because it explicitly includes the effects of bond breaking, such as the existence of unbound states. It also accounts for the anharmonicity of real bonds and the non-zero transition probability for overtone and combination bands. Product highlight
Potential Energy FunctionThe Morse potential energy function is of the form
Here r is the distance between the atoms, re is the equilibrium bond distance, De is the well depth (defined relative the dissociated atoms), and a controls the 'width' of the potential. The dissociation energy of the bond can be calculated by subtracting the zero point energy E(0) from the depth of the well. The force constant of the bond can be found by taking the second derivative of the potential energy function, from which it can be shown that the parameter, a, is
where ke is the force constant at the minimum of the well. Of course, the zero of potential energy is arbitrary, and the equation for the Morse potential can be rewritten any number of ways by adding or subtracting a constant value. Vibrational EnergyStationary states on the Morse potential have eigenvalues where v is the vibrational quantum number, and ν0 has units of frequency, and is mathematically related to the particle mass, m, and the Morse constants via
Whereas the energy spacing between vibrational levels in the quantum harmonic oscillator is constant at hv0, the energy between adjacent levels decreases with increasing v in the Morse oscillator. Mathematically, the spacing of Morse levels is
This trend matches the anharmonicity found in real molecules. However, this equation fails above some value of v where E(v + 1) − E(v) is calculated to be zero or negative. This failure is due to the finite number of bound levels in the Morse potential, and some maximum v, vm that remains bound. For energies above vm, all the possible energy levels are allowed and the equation for E(v) is no longer valid. Below vm, E(v) is a good approximation for the true vibrational structure in non-rotating diatomic molecules. In fact, the real molecular spectra are generally fit to the form1 in which the constants ωe and ωeχe can be directly related to the parameters for the Morse potential. Solving Schrödinger's equation for the Morse oscillatorLike the quantum harmonic oscillator, the energies and eigenstates of the Morse potential can be found using operator methods. One approach involves applying the factorization method to the Hamiltonian. See alsoReferences
Categories: Chemical bonding | Quantum chemistry |
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Morse_potential". A list of authors is available in Wikipedia. |





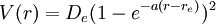 .
.
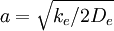 ,
,
![E(v) = h\nu_0 (v+1/2) - \frac{\left[h\nu_0(v+1/2)\right]^2}{4D_e}](images/math/3/1/6/316542e24f3eb81a6dcbad51090b4e87.png)
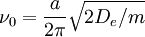 .
.
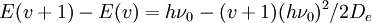 .
.