To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Diatomic molecule
Diatomic molecules are molecules made only of two atoms, of either the same or different chemical elements. The prefix di- means two in Greek. Product highlight
Description and occurrence in natureHuber and Herzberg's book, Molecular Spectra and Molecular Structure IV. Constants of Diatomic Molecules[1], lists hundreds of diatomic molecules, some which have been detected spectroscopically in interstellar space. However, few diatomics are found to occur naturally on Earth outside of laboratories. About 99% of the Earth's atmosphere is composed of diatomic molecules, specifically oxygen O2 (21%) and nitrogen N2 (78%), with the remaining 1% being mostly argon (0.9340%). The natural abundance of hydrogen (H2) in the Earth's atmosphere is only on the order of parts per million, but H2 is, in fact, the most abundant molecule seen in nature, dominating the composition of stars. Elements that consist of diatomic molecules, under typical laboratory conditions of 1 bar and 25 oC, include hydrogen (H2), nitrogen (N2), oxygen (O2), and the halogens: fluorine (F2), chlorine (Cl2), bromine (Br2), iodine (I2), and, perhaps, astatine (At2).[2] Again note that many other diatomics are possible, such as metals heated to their gaseous states. Also, many diatomic molecules are unstable and highly reactive, such as diphosphorus. A few compounds are made of diatomic molecules, including CO and HBr. If a diatomic molecule consists of two atoms of the same element, such as H2 and O2, then it is said to be homonuclear, but otherwise it is said to heteronuclear, such as with CO or NO. The bond in a homonuclear diatomic molecule is non-polar and fully covalent. Historical significanceDiatomic elements played an important role in the elucidation of the concepts of element, atom, and molecule in the 19th century, because some of the most common elements, such as hydrogen, oxygen, and nitrogen, occur as diatomic molecules. John Dalton's original atomic hypothesis assumed that all elements were monatomic and that the atoms in compounds would normally have the simplest atomic ratios with respect to one another. For example, Dalton assumed that water's formula was HO, giving the atomic weight of oxygen as 8 times that of hydrogen, instead of the modern value of about 16. As a consequence, confusion existed regarding atomic weights and molecular formulas for about half a century. As early as 1805, Gay-Lussac and von Humboldt showed that water is formed of two volumes of hydrogen and one volume of oxygen, and by 1811 Amedeo Avogadro had arrived at the correct interpretation of water's composition, based on what is now called Avogadro's law and the assumption of diatomic elemental molecules. However, these results were mostly ignored until 1860. Part of this rejection was due to the belief that atoms of one element would have no chemical affinity towards atoms of the same element, and part was due to apparent exceptions to Avogadro's law that were not explained until later in terms of dissociating molecules. At the 1860 Karlsruhe Congress on atomic weights, Cannizzaro resurrected Avogadro's ideas and used them to produce a consistent table of atomic weights, which mostly agree with modern values. These weights were an important pre-requisite for the discovery of the periodic law by Dmitri Mendeleev and Lothar Meyer.[3]
Energy levelsIt is convenient, and common, to represent a diatomic molecule as two point masses (the two atoms) connected by a massless spring. The energies involved in the various motions of the molecule can then be broken down into three categories.
Translational energiesThe translational energy of the molecule is simply given by the kinetic energy expression: where m is the mass of the molecule and v is its velocity. Rotational energiesClassically, the kinetic energy of rotation is
For microscopic, atomic-level systems like a molecule, angular momentum can only have specific discrete values given by
Also, for a diatomic molecule the moment of inertia is
So, substituting the angular momentum and moment of inertia into Erot, the rotational energy levels of a diatomic molecule are given by: Vibrational energiesAnother way a diatomic molecule can move is to have each atom oscillate - or vibrate - along a line (the bond) connecting the two atoms. The vibrational energy is approximately that of a quantum harmonic oscillator:
Comparison between rotational and vibrational energy spacingsThe lowest rotational energy level of a diatomic molecule occurs for l = 0 and gives Erot = 0. For O2, the next highest quantum level (l = 1) has an energy of roughly: This spacing between the lowest two rotational energy levels of O2 is comparable to that of a photon in the microwave region of the electromagnetic spectrum. The lowest vibrational energy level occurs for n = 0, and a typical vibration frequency is 5 x 1013 Hz. Doing a calculation similar to that above gives:
So the spacing, and the energy of a typical spectroscopic transition, between vibrational energy levels is about 100 times greater than that of a typical transition between rotational energy levels. See also
Further reading
Notes and references
|
|||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Diatomic_molecule". A list of authors is available in Wikipedia. |





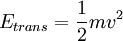
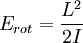
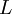 is the angular momentum
is the angular momentum
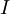 is the moment of inertia of the molecule
is the moment of inertia of the molecule
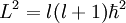
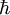 is Planck's reduced constant.
is Planck's reduced constant.
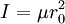
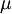 is the reduced mass of the molecule and
is the reduced mass of the molecule and
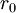 is the average distance between the two atoms in the molecule.
is the average distance between the two atoms in the molecule.
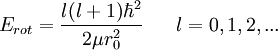
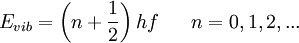
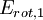
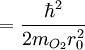
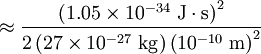
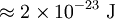
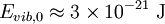 .
.


