To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Stagnation point
Product highlightThe stagnation point is a point on the surface of a body submerged in a fluid flow where the fluid velocity is zero. The Bernoulli equation shows that the static pressure is highest when the velocity is zero. The velocity is zero at stagnation points so the pressure around the submerged body is highest at the stagnation points. This pressure is called the stagnation pressure. The Bernoulli equation shows that the stagnation pressure is equal to the dynamic pressure plus free-stream static pressure. We can use this information in the equation for finding pressure coefficient Cp: where:
Stagnation pressure minus static pressure is equal to dynamic pressure; therefore the pressure coefficient Cp at stagnation points is 1. On a streamlined body fully immersed in a potential flow, there are two stagnation points. On a body with a sharp point such as the trailing edge of a wing, the Kutta condition specifies that a stagnation point is at that location. The streamline at a stagnation point is perpendicular to the surface of the body. |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Stagnation_point". A list of authors is available in Wikipedia. |





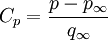
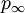 is pressure at points remote from the body (free-stream static pressure)
is pressure at points remote from the body (free-stream static pressure)
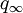 is
is 

