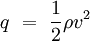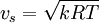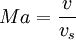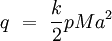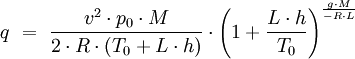Dynamic pressure

In fluid dynamics dynamic pressure (indicated with q, or Q, and sometimes called velocity pressure) is the quantity defined by:

Additional recommended knowledge

Guide to balance cleaning: 8 simple steps

Weighing the right way

Daily Visual Balance Check

where (using SI units):

q = dynamic pressure in pascals

ρ = fluid density in kg/m³ (e.g. density of air)

v = fluid velocity in m/s

Physical meaning

Dynamic pressure is closely related to the kinetic energy of a fluid particle, since both quantities are proportional to the particle's mass (through the density, in the case of dynamic pressure) and square of the velocity. Dynamic pressure is in fact one of the terms of Bernoulli's equation, which is essentially an equation of energy conservation for a fluid in motion.

Another important aspect of dynamic pressure is that, as dimensional analysis shows, the aerodynamic stress (i.e. stress within a structure subject to aerodynamic forces) experienced by an aircraft traveling at speed v is proportional to the air density and square of v, i.e. proportional to q. Therefore, by looking at the variation of q during flight, it is possible to determine how the stress will vary and in particular when it will reach its maximum value. The point of maximum aerodynamic load is often referred to as max Q and it is a critical parameter, for example, for spacecraft during launch.

Alternative forms

If the fluid in question can be considered an ideal gas (which is generally the case for air), the dynamic pressure can be expressed as a function of fluid pressure and Mach number.

By applying the ideal gas law:

p = ρRT

the definition of speed of sound:

and the definition of Mach number:

dynamic pressure can be rewritten as:

where (using SI units):

p = pressure in pascals

Ma = non-dimensional Mach number

ρ = density in kg/m³

R = specific gas constant (287.05 J/(kg·K) for air)

T = absolute temperature in kelvin

k = non-dimensional heat capacity ratio (1.4 for air, constant)

v = speed in m/s

v_s = speed of sound in m/s

Alternatively, considering for example a spacecraft during launch and using the formula for the air density as a function of altitude (only valid below the tropopause), the dynamic pressure associated with the spacecraft can be expressed as:

where (using SI units):

q = dynamic pressure in pascals

v = spacecraft's velocity in m/s

p₀ = atmospheric pressure at sea level in pascals

M = molecular weight of dry air (0.0289644 kg/mol)

R = specific gas constant (287.05 J/(kg·K) )

T₀ = absolute air temperature at sea level in kelvin

L = atmospheric temperature lapse rate (−0.0065 K/m)

h = altitude above sea level in m

g = acceleration due to gravity at the Earth's surface in (9.80665 m/s²)

See also

• Pressure