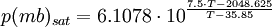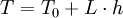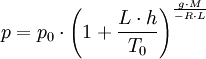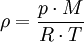To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Density of airThe density of air, ρ (Greek: rho) (air density), is the mass per unit volume of Earth's atmosphere, and is a useful value in aeronautics. As does air pressure, air density decreases with increasing altitude and temperature. At sea level and at 20 °C, dry air has a density of approximately 1.2 kg/m3 (0.002377 slug/ft3). The density of water, which is about 1000 kg/m3 (1 g/cm³), is about 800 times more than the density of air. Product highlight
Effects of temperature and pressureThe formula for the density of dry air is given by: where ρ is the air density, p is pressure, R is the specific gas constant, and T is temperature in kelvins. The specific gas constant R for dry air is: Therefore:
Effect of water vaporThe addition of water vapor to air (making the air humid) reduces the density of the air, which may at first appear contrary to logic. This occurs because the molecular mass of water (18) is less than the molecular mass of air (around 29). For any gas, at a given temperature and pressure, the number of molecules present is constant for a particular volume. So when water molecules (vapor) are introduced to the air, the number of air molecules must reduce by the same number in a given volume, without the pressure or temperature increasing. Hence the mass per unit volume of the gas (its density) decreases. The density of humid air may be calculated as a mixture of ideal gases. In this case, the partial pressure of water vapor is known as the vapor pressure. Using this method, error in the density calculation is less than 0.2% in the range of −10 °C to 50 °C. The density of humid air is found by: Where:
The vapor pressure of water may be calculated from the saturation vapor pressure and relative humidity. It is found by: Where:
The saturation vapor pressure of water at any given temperature is the vapor pressure when relative humidity is 100%. A simplification of the regression [1] used to find this, can be formulated as: IMPORTANT:
Where p simply notes the absolute pressure in the observed system. Effects of altitudeTo calculate the density of air as a function of altitude, one requires additional parameters. They are listed below, along with their values according to the International Standard Atmosphere, using the universal gas constant instead of the specific one:
Temperature at altitude h meters above sea level is given by the following formula (only valid inside the troposphere): The pressure at altitude h is given by: Density can then be calculated according to a molar form of the original formula: Importance of temperatureThe below table demonstrates that the properties of air change significantly with temperature. Table — speed of sound in air c, density of air ρ, acoustic impedance Z vs. temperature °C
See alsoReferences |
|||||||||||||||||||||||||||||||||||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Density_of_air". A list of authors is available in Wikipedia. | |||||||||||||||||||||||||||||||||||||||||||||





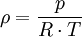
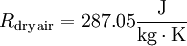
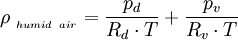
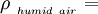 Density of the humid air (kg/m³)
Density of the humid air (kg/m³)
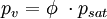
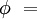 Relative humidity
Relative humidity