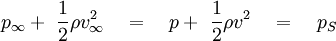In fluid mechanics, and in particular in fluid statics, static pressure [1] is the pressure exerted by a fluid at rest[citation needed].[2]
Examples of situations where static pressure is involved are:
- The air pressure inside a latex balloon is the static pressure and so is the atmospheric pressure (neglecting the effect of wind).
- The hydrostatic pressure at the bottom of a dam is by definition the static pressure and so is the pressure exerted on one's thumb when stopping the water flow in a garden hose.
- The pressure inside a ventilation duct is not the static pressure, unless the air inside the duct is still.
- On an aircraft in flight, the pressure measured on a generic point of the surface of the wing (or fuselage) is not, in general, the static pressure.[3]
Static pressure in fluid dynamics
The use of the expression static pressure in fluid dynamics is very common, although it can lead to ambiguity. The ambiguity arises from the fact that static pressure can be used, correctly, to refer to the free-stream pressure in external flows, but it is more often, and not always correctly, used to refer to the pressure in a generic point of a flow field, typically when discussing the Bernoulli equation. In order to avoid ambiguity, alternative expressions that could be used, depending on the context, are free-stream pressure, fluid pressure, thermodynamic pressure or often just pressure.
Equivalence of static and free-stream pressure
We consider as an example the atmosphere, at rest relatively to the ground. An observer standing on the ground would see a generic fluid element as not moving, and subject to the local static pressure (which, in this case, is the atmospheric pressure).
We now consider an aircraft that flies straight and level with speed 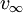 (airspeed and ground speed are the same, in this example), approaching the same fluid element from great distance. The distance is such that the fluid element is not perturbed by the approaching aircraft. To an observer on board the aircraft, the fluid element, like all the fluid elements at the same distance, appears as being in free-stream conditions, where all the fluid elements flow straight towards the aircraft with the same constant velocity (airspeed and ground speed are the same, in this example), approaching the same fluid element from great distance. The distance is such that the fluid element is not perturbed by the approaching aircraft. To an observer on board the aircraft, the fluid element, like all the fluid elements at the same distance, appears as being in free-stream conditions, where all the fluid elements flow straight towards the aircraft with the same constant velocity 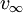 and there are no pressure gradients inside the fluid (that is the pressure is constant anywhere in that region of fluid).[4] Given that the fluid element is the same for both observers, so is the pressure to which the element is subject, therefore what an observer at rest calls static pressure is in fact the free-stream pressure to an observer moving relatively to the fluid. This is the only case in fluid dynamics where, strictly speaking, the expression static pressure can be used appropriately[citation needed], i.e. to refer to the free-stream pressure. and there are no pressure gradients inside the fluid (that is the pressure is constant anywhere in that region of fluid).[4] Given that the fluid element is the same for both observers, so is the pressure to which the element is subject, therefore what an observer at rest calls static pressure is in fact the free-stream pressure to an observer moving relatively to the fluid. This is the only case in fluid dynamics where, strictly speaking, the expression static pressure can be used appropriately[citation needed], i.e. to refer to the free-stream pressure.
Note that when the fluid element comes in proximity to the aircraft, free-stream conditions are lost, its velocity changes and pressure gradients develop. The pressure exerted on the element, therefore, will not be, in general, equal to the static pressure anymore.
Static pressure and the Bernoulli equation
The Bernoulli equation, assuming incompressible, inviscid flow and negligible gravitational effects, can be written as follows:
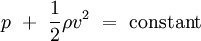
Since the term ρv2 / 2 is, by definition, the so-called dynamic pressure, the term p, by contrast, is usually named static pressure although it may, or may not, refer to the above mentioned free-stream pressure. The two possible cases are:
- Bernoulli equation referred to free-stream conditions – When the Bernoulli equation is applied to a point of the flow field far upstream of any object, both pressure and velocity take their respective free-stream values
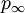 and and 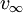 , therefore the Bernoulli equation can be correctly read as "the sum of static pressure and (free-stream) dynamic pressure is constant across the flow field". , therefore the Bernoulli equation can be correctly read as "the sum of static pressure and (free-stream) dynamic pressure is constant across the flow field".
- Bernoulli equation referred to a generic point – When the Bernoulli equation is written for a generic point A of the flow field, for example a point close to an airfoil, the value of the fluid pressure pA is in general different from the free-stream one, and, strictly speaking, the term should not be referred to as static pressure. The Bernoulli equation could be correctly read, for example, as "the sum of fluid pressure in A and dynamic pressure in A is constant across the flow field". Nevertheless it is very common to refer to the non-velocity-dependent term of the Bernoulli equation as static pressure anyway, regardless of whether it is applied to free-stream conditions or not.
The two cases can be summarized by applying the Bernoulli equation to different points of the flow field: a point far upstream, a generic point close to a body and, for completeness, a stagnation point on the body's surface:
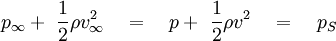
where:
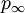 = free-stream (static) pressure = free-stream (static) pressure
- ρ = fluid density (assumed constant)
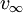 = free-stream velocity = free-stream velocity
- p = fluid pressure in a generic point
- v = velocity in a generic point
- pS = stagnation (or total) pressure
See also
References
- ^ From Greek στατικός (IPA: [statiˈkos]), causing to stand.
- ^ From Dictionary.com static: acting by mere weight without producing motion: static pressure.
- ^ There are only a few areas (e.g. some parts of the fuselage or along the outside of a Pitot tube) where the pressure exerted is equal to the static pressure; those are the places where static ports are located.
- ^ A pressure gradient would in fact cause an acceleration, and so the velocity would not be constant anymore. Note also that we are neglecting the variation of atmospheric pressure with altitude.
|





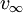 (airspeed and ground speed are the same, in this example), approaching the same fluid element from great distance. The distance is such that the fluid element is not perturbed by the approaching aircraft. To an observer on board the aircraft, the fluid element, like all the fluid elements at the same distance, appears as being in free-stream conditions, where all the fluid elements flow straight towards the aircraft with the same constant velocity
(airspeed and ground speed are the same, in this example), approaching the same fluid element from great distance. The distance is such that the fluid element is not perturbed by the approaching aircraft. To an observer on board the aircraft, the fluid element, like all the fluid elements at the same distance, appears as being in free-stream conditions, where all the fluid elements flow straight towards the aircraft with the same constant velocity 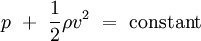
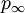 and
and