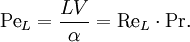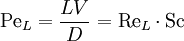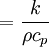Péclet number

In fluid dynamics, the Péclet number is a dimensionless number relating the rate of advection of a flow to its rate of diffusion, often thermal diffusion. It is equivalent to the product of the Reynolds number with the Prandtl number in the case of thermal diffusion, and the product of the Reynolds number with the Schmidt number in the case of mass diffusion.

Additional recommended knowledge

Essential Laboratory Skills Guide

What is the Sensitivity of my Balance?

Don't let static charges disrupt your weighing accuracy

For thermal diffusion, the Péclet number is defined as:

For mass diffusion, it is defined as:

where

• L - characteristic length
• V - Velocity
• α - Thermal diffusivity
• D - mass diffusivity

and

• k - Thermal conductivity
• ρ - Density
• c_p - Heat capacity

In engineering applications the Péclet number is often very large. In such situations, the dependency of the flow upon downstream locations is diminished, and variables in the flow tend to become 'one-way' properties. Thus, when modelling certain situations with high Péclet numbers, simpler computational models can be adopted.^[1]

A flow will often have different Péclet numbers for heat and mass. This can lead to the phenomenon of Double-diffusive convection.

See also

• Reynolds number
• Prandtl number
• Schmidt number

References

1. ^ Patankar, Numerical Heat Transfer and Fluid Flow, ISBN 0891165223, p 102