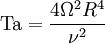My watch list

Taylor number

In fluid dynamics, the Taylor number is a dimensionless quantity that characterizes the importance of centrifugal "forces" or so-called inertial forces due to rotation of a fluid about a vertical axis, relative to viscous forces. The typical context of the Taylor number is in characterization of the Couette flow between rotating colinear cylinders or rotating concentric spheres. In the case of a system which is not rotating uniformly, such as the case of cylindrical Couette flow in the case where the outer cylinder is stationary and the inner cylinder is rotating, inertial forces will often tend to destabilize a system, whereas viscous forces tend to stabilize a system and damp out perturbations and turbulence.

Additional recommended knowledge

Weighing the right way

Better weighing performance in 6 easy steps

Safe Weighing Range Ensures Accurate Results

On the other hand, in other cases the effect of rotation can be stabilizing. For example, in the case of cylindrical Couette flow with positive Rayleigh discriminant, there are no axisymmetric instabilities. Another example is a bucket of water that is rotating uniformly (i.e. undergoing solid body rotation). Here the fluid is subject to the Taylor-Proudman theorem which says that small motions will tend to produce purely two-dimensional perturbations to the overall rotational flow. However, in this case the effects of rotation and viscosity are usually characterized by the Ekman number and the Rossby number rather than by the Taylor number.

There are various definitions of the Taylor number which are not all equivalent, but most commonly it is given by

$\mathrm{Ta}=\frac{4\Omega^2 R^4}{\nu^2}$

where $Ω$ is a characteristic angular velocity, $R$ is a characteristic linear dimension perpendicular to the rotation axis, and $ν$ is the kinematic viscosity.

In the case of inertial instability such as Taylor-Couette flow, the Taylor number is mathematically analogous to the Rayleigh number which characterizes the strength of buoyant forces relative to viscous forces in convection. When the former exceeds the latter by a critical ratio, convective instability sets in. Likewise, in various systems and geometries, when the Taylor number exceeds a critical value, inertial instabilities set in, sometimes known as Taylor instabilities, which may lead to Taylor vortices or cells.

Taylor refers to the British physicist Geoffrey Ingram Taylor (1886-1975).

Category: Fluid dynamics